変分ベイズを使って変化点検知をしてみる
おつかれさまです.今回は簡単なメッセージ受信数のデータを使って,変分ベイズによる変化点検知をやってみたいと思います.なお,今回使うデータやモデルは下記のPyMCの入門書を参考にしています*1.
Pythonで体験するベイズ推論-PyMCによるMCMC入門-キャメロン-デビッドソン-ピロン
この本では推論にMCMCを使っていますが,今回はモデルはそのまま流用し,同じことを実現する変分ベイズによる近似推論を導いてみます. 一般的には変分ベイズの方が計算が高速なので,MCMCの性能に満足できない場合などは変分ベイズは良い代替手法になり得ます.また,今回紹介する例は,過去に紹介した混合モデルを使った例よりも比較的シンプルですので,変分ベイズの入門題材にはちょうど良いんじゃないかと思っています.
MCMCによる変化点検知
・メッセージ受信データ
PyMC本では次のような「ある期間で受信したメール数」を題材にMCMCを解説しています.

データをよーく見てみると,非常に微妙ではありますが,経過日数の後半の方で受信メッセージ数が少し多くなっているような傾向が見えます.この変化点をベイズモデリングによって見つけるのが目標です.
・モデル
n日目のメッセージ受信数Cnはカウントデータなので,次のようなポアソン分布を使ってモデル化するのが良いでしょう.

ここで,λはポアソン分布の平均パラメータです.また,次のようにある日目を境にこの平均パラメータが変化することを仮定します.

それぞれのパラメータλ1およびλ2はポアソン分布の共役事前分布であるガンマ分布を使ってモデル化します*2.

PyMC本ではデータの平均値を使って超パラメータを設定していますが,あんまりおすすめしません. 僕は適当にa,bの値を設定した後にモデルからデータをサンプルしてみて,なんとなくスケール観が合ってそうな値(a=2.0, b=0.1)に設定しておきました.
最後に,変化点は次のように全部でN日の中から等確率で選ばれると仮定します.
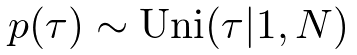
・MCMCによる推論
詳しくは本やJupyter Notebookの内容を参考にしてほしいのですが,モデル(model)をPyMCで構築した後に次のようなコードを書くと事後分布からのサンプルが得られます.
iters = 40000 burn = 10000 mcmc = pm.MCMC(model) mcmc.sample(iters, burn)
mcmc.sampleを叩いたあと,数秒待つと,各変数のサンプルが取り出せます.
lambda_1_samples = mcmc.trace("lambda_1")[:] lambda_2_samples = mcmc.trace("lambda_2")[:] tau_samples = mcmc.trace("tau")[:]
得られたサンプルを元に各種期待値を計算すると,次のようになりました.
 上図ではサンプルから計算される各日のλの期待値をプロットしています.下図では,各日におけるτの近似事後確率を示しています.
確かに,45日目あたりを境に,メッセージ受信数の傾向が微増していることが示唆されていますね.ちなみに,iters=5000より小さい値を設定すると,あんまり綺麗な分布は得られませんでした.
上図ではサンプルから計算される各日のλの期待値をプロットしています.下図では,各日におけるτの近似事後確率を示しています.
確かに,45日目あたりを境に,メッセージ受信数の傾向が微増していることが示唆されていますね.ちなみに,iters=5000より小さい値を設定すると,あんまり綺麗な分布は得られませんでした.
変分ベイズによる変化点検知
・変分ベイズ(平均場近似版)の概要
平均場近似による変分ベイズの導出方法を簡単におさらいしましょう.データXを観測したあとの潜在変数(パラメータ含む)Z1,Z2の事後分布を次のように近似するとします.

Z1,Z2の事後分布を同時分布として表現することは諦め,よりシンプルな独立の分布qで近似しようというのがアイデアです.近似分布qを真の分布に「似せる」ために,次のようなKLダイバージェンスをqに関して最小化します.

詳しくはこちらの記事に書いてありますが,結果としては次のような式を繰り返し計算すればKLダイバージェンスが徐々に小さくなっていくことになります.

今回はこの結果をそのまま使って,変分ベイズのアルゴリズムを導出します.
・更新アルゴリズムの導出
さて,先ほどのメッセージ受信数の変化モデルから,変分ベイズを導いてみることにしましょう.次のように,少しだけモデルを計算しやすく書き直してみます.

ここで,δ()は中身が真の場合は1を返し,そうでない場合は0を返すような関数です.τの値によってデータがサンプルされる分布が切り替わるイメージですね.
次に,このモデルの事後分布の分解を次のように仮定します.

ここまで決めてしまえば,あとは機械的に計算をするだけです.λ1の近似事後分布は,
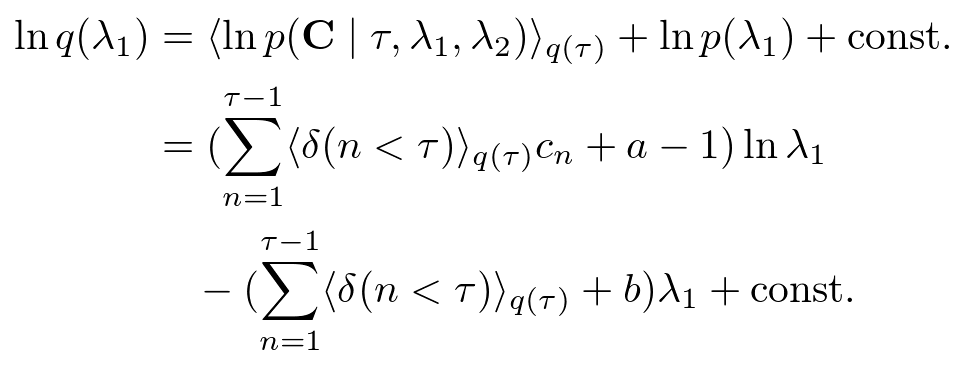
となるので,


とガンマ分布で表現出来ます.λ2もまったく同様に,


となります. 次にτの近似事後分布は,

となるので,次のような離散分布になります.

また,近似事後分布がガンマ分布と離散分布(カテゴリ分布)であることがわかったので,途中計算に必要な期待値も次のように求められます.
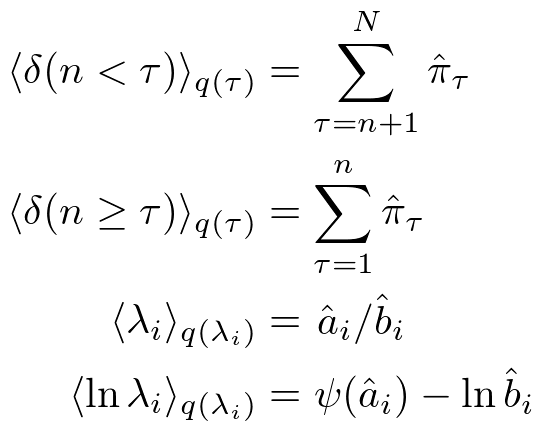
・動かしてみる
さて,先ほどのアルゴリズムを使って事後分布を推定した結果は次のようになります,
 PyMCで十分なサンプル数で実行した場合とほとんど同じ結果になりましたね.ただ,変分ベイズの場合はこの近似分布を得るまでにMAXITER=5程度でほぼ完全に収束し,計算時間も一瞬でした.
PyMCで十分なサンプル数で実行した場合とほとんど同じ結果になりましたね.ただ,変分ベイズの場合はこの近似分布を得るまでにMAXITER=5程度でほぼ完全に収束し,計算時間も一瞬でした.
せっかくなので,適当に作ったトイデータで同じように推論してみます.
 上図からわかるように,変化点がはっきり見えているようなデータなので,下図ではアルゴリズムも確率ほぼ1.0という強い自信を持って変化日が50日目だと言っていますね.
上図からわかるように,変化点がはっきり見えているようなデータなので,下図ではアルゴリズムも確率ほぼ1.0という強い自信を持って変化日が50日目だと言っていますね.
データを作り直してもう1回やってみましょう.
 このデータはちょっと意地悪だったかもしれません.データからはまったく変化点を見ることが出来ません.
下図の結果では「どこかが変化日だったのかわかりません」と言っています.なかなか良い答えです.無理くりどこかを予測結果として出されるより,よっぽど紳士的ですね*3.
このデータはちょっと意地悪だったかもしれません.データからはまったく変化点を見ることが出来ません.
下図の結果では「どこかが変化日だったのかわかりません」と言っています.なかなか良い答えです.無理くりどこかを予測結果として出されるより,よっぽど紳士的ですね*3.
Juliaで実装したソースコードは下記に置いてあります.(change_point.jl)
MLBlog/src at master · sammy-suyama/MLBlog · GitHub
ということで,本日は以上です.
*1:英語になっちゃいますが,本の内容とほぼ同じJupyter Notebookがあります. https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers
*2:PyMC本では指数分布を使っていますが,ガンマ分布でa=1とおけば指数分布に一致します.
*3:今回のモデルは,「変化点は確実に1つあるんだけど,どこかわからない」という前提のもとで推論をする話になっています.最後の結果は「変化点はありませんでした」とは違うことに注意してください.