ベイズ推論による機械学習の基本

今回は基本的なベイズ学習の概念と流れを説明したいと思います。まず始めに、ベイズ学習のすべての基本となる２つの計算規則（和の規則、積の規則）を取り上げます。また、ベイズ学習に関わるややこしい用語たち（データ、尤度関数、事前分布、事後分布、エビデンス、予測分布、などなど）に関しても念のためここで整理しておきたいと思います。そして最後に、簡単な多次元のガウス分布とウィシャート分布を使ったベイズ推論の例を取り上げ、それぞれの用語や概念との具体的な結びつきについて触れたいと思っています。

・ベイズ学習の基本概念

さて、確率モデルを使ったベイズ推論を行う上で最小限必要なのは次のたった２つの計算ルールです。

<和の規則>

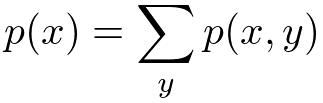
<積の規則>

 

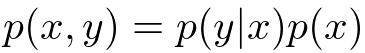
は同時分布（joint distribution）、は条件付き分布（conditional distribution）と呼ぶんでした。極端な言い方をしてしまうと、ベイズ推論による機械学習のすべては、この2つのルールをいかに効率よく用いることによって未知の確率分布を計算するかということに尽きてしまいます。

さて、もう少し踏み込んでみましょう。まず最初に、上の2つの規則を組み合わせることによって次のような有名なベイズの定理（Bayes's theorem）を得ることができます。

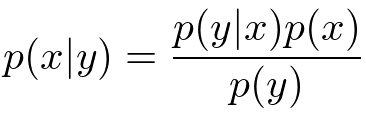
で表される確率分布を、逆にしたやその他の項の組み合わせで表現できてしまうというのがこの式の言わんとすることです。このことから、ベイズ推論は逆確率の法則なんて呼ばれたりもするみたいです。

ここでようやく機械学習らしい概念を導入してみることにします。といってもちょっと用語を導入してみるだけです。の代わりにを、の代わりにを文字として用いると、ベイズの定理は次のようになります。

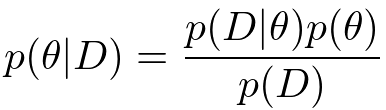
 ここではデータ、はパラメータと呼ぶことにします。

さて、データに関しては説明は要らないでしょう。写真データとか、人の声の録音データとか、月間の製品の売り上げデータとかなんでも想像しやすいものでＯＫです。データは複数そろっていることを基本的には想定しますが、実は1個でも0個でも大丈夫だったりします。

は一般的にはパラメータと呼ばれます。 ベイズ学習においてパラメータは推論すべき未知の変数として扱われます*1。

さて、改めてこの重要な式をじっくり見てみることにしましょう。まずは尤度関数（likelihood function）と呼ばれています。パラメータがある特定の値に条件づけされたときに、データがどれだけモデルから発生しやすいかを表現しています。その後ろについているは事前分布（prior distribution）と呼ばれており、の分布に関する我々の事前の仮説（どんなが出やすいのか？）を表現しています*2。それに対して一番左の式は事後分布（posterior distribution）と呼ばれています。こちらも事前分布と同様パラメータの不確かさを表す確率分布ですが、データによって条件づけされているところが違いますね。この分布は尤度関数を通すことによって更新されたの分布というふうに解釈することができます。ベイズ学習の主要な課題はこの事後分布をいかに効率よく、精度高く計算するかにあります。

さて、尤度関数と事前分布の掛け算をしただけでは事後分布の計算は完了しません。分母にもう１つ項がついていますね。これはエビデンス（evidence）あるいは周辺尤度（marginal likelihood）呼ばれており、事後確率がちゃんと正規化される（＝分布を積分すると１になる）ことを保証するために必要になってくる項です。エビデンスは和の規則を用いることによって次のように計算することができます。

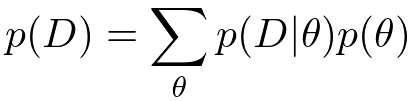
「分子の項におけるを和の規則で除去しなさい」と言っているんですね。簡単なガウス分布などを使ったモデルであればこの項は解析的に計算できるのですが、少し複雑なモデルになってくるとこの和が計算できなくなってしまいます。離散の場合は組み合わせ爆発を起こし、連続の場合には積分が解析不可能になってしまいます。ちなみにこのモデルエビデンスの値を使って複数のモデルの良し悪しを直接決めることもあるようです（モデル選択*3）。

さて、最後にもう1つ大事な概念を紹介してみましょう。機械学習では、ある学習データを使ってモデルを訓練させ、新しいデータに対して予測を行う、というのが代表的なアプリケーションになります。したがって、次のような新しいデータに関する予測分布（predictive distribution）を計算することも重要な課題の1つです。

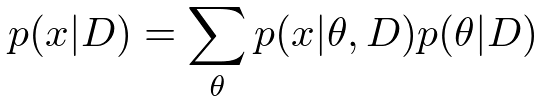
事後分布（学習済みのパラメータの分布）を使って、まだ入ってきていない新データに関する確率分布（平均とか分散とか）を計算しようというわけです。

ここまでのベイズ学習における基本的な流れをまとめてみると次のようになります。*4

１、尤度関数（観測データの表現方法）を定義する。

２、事前分布（パラメータの散らばり具合）を設定する。

３、ベイズの定理を使って事後分布を更新する。（＝学習）

４、事後分布から予測分布を計算し、未知の値の確率分布を求める。（＝予測）

・ガウス分布とウィシャート分布を使った具体例

ちょっと抽象的な話が続いてしまったので、次は具体的なモデルの例を当てはめて話を進めたいと思います。今回は、Ｄ次元、Ｎ個の観測データをとおくことにします。尤度関数と事前分布は具体的には次のように定義してみたいと思います。

<尤度関数（ガウス分布）>

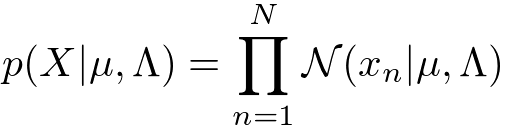
＜事前分布（ガウス・ウィシャート分布）＞

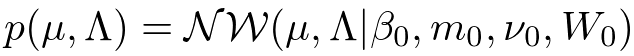
ガウス分布（Gauss distribution）はデータに対するノイズを表現する上で最も一般的に使われているモデルの1つです。ガウス分布には2つのパラメータ（平均）と（精度行列）がありますが、ベイズ学習ではこれらは確率変数として扱われます。したがって確率分布が必要になってくるのですが、今回は計算が解析的になるという理由で共役事前分布（conjugate prior distribution）のガウス・ウィシャート分布（Gauss-Wishart distribution）を用いることにします。ちなみに、、、といった文字は超パラメータ（hyper parameter）と呼ばれており、事前分布の形状を決定するものになります。これらは確率変数として扱われず、固定された値を持ちます。

さて、ここまでが準備段階です。次にこのモデルを使ってデータを「学習」してみたいと思います。もっと丁寧に言うと、ベイズ学習における「学習」とは、データを観測した後の、パラメータの事後分布を計算することに対応します。今は非常に基本的なガウスモデルを使っているので、特に最適化やサンプリングなど凝ったテクニックは必要とせずに解析的に手計算することができ、得られる分布は事前分布と同じ形状（ガウス・ウィシャート分布）を持ったものになります。

具体的には、次のようにベイズの定理の分子だけを使ってとの関数を求めてあげると、いくらか計算が楽です。

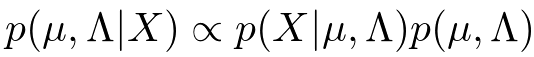
得られた式を正規化してあげることにより、ガウス・ウィシャート分布が得られれます。

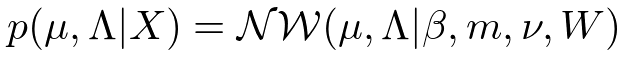
分布の形状を決めるそれぞれの超パラメータは事後分布では次のような計算結果になります。

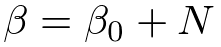
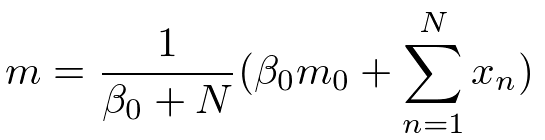
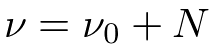
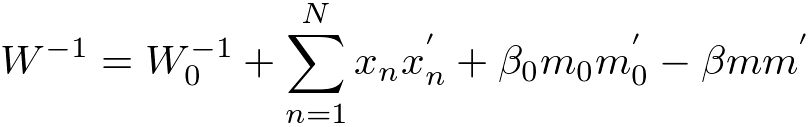
計算過程は省きましたが、このような結果が自分ですらすら計算できるようになるとベイズ学習の入門コース卒業になります。

それでは次に予測分布も求めてみましょう。一般的にはパラメータの分布を学習しただけで満足するケースはあまりなく、学習後のモデルを使って何らかの予測を行うことが機械学習における主要なテーマになってきます。

さて、予測分布の計算は未観測のデータに対する尤度関数と事後分布を掛け合わせ、パラメータだけを積分除去すれば得られるんでした。さっそく計算してみましょう。

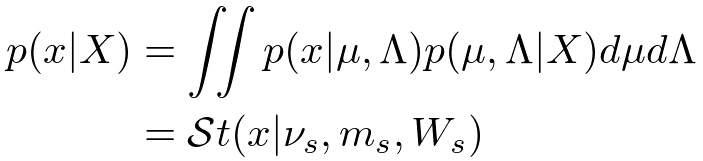
ガウス分布の平均パラメータと精度パラメータを両方とも積分除去しなければならないので若干計算がめんどくさいですが、結果は解析的に計算でき、スチューデントのｔ分布（Student's t-distribution）が得られます。それぞれの超パラメータは次のようになります。

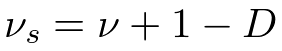
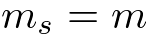
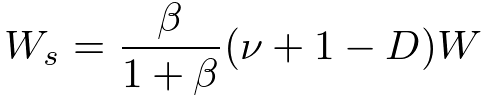
・まとめ

今回はベイズ推論を使った機械学習の基本的な流れに関して説明しました。単純な線形回帰モデルなんかは今日の結果を利用すれば比較的簡単に構築することができます。一方で線形識別（ロジスティック回帰など）は前述の積分計算が解析的に実行することができず、ラプラス近似などの近似手法を使う必要があります。またクラスタリング等で使われる混合モデルや時系列データを取り扱うためのＨＭＭなんかも、一般的には解析計算ができないので変分近似やサンプリングなどの近似手法に頼ることになります。ただこれらは単に計算上の問題なので、基本的には上述のベイズの定理を使った学習の枠組みを使って事後分布を計算するという流れは変わりません。

今回の記事がよくわからん！という方には，次のような入門書もあります．

books.rakuten.co.jp

*1: ”パラメータ”という用語はなんだか固定された値のように聞こえてしまうことがあります。最近では今回の記事のようなを（すべてのデータ点に共有される確率変数という意味で）”大域確率変数（global variable）”と呼んだりすることもあるようです。

*2:事前分布は基本的にデータを観測する前に決めてあげなければいけません。具体的にどのような事前分布を選んだらいいのかは、また別の機会でお話しします。

*3:ちなみに究極のベイジアンはモデル選択すらしません。仮説（あるいはモデル）Hが複数個あった場合、P(X) = ΣP(X|H)P(H)のようにすべての仮説を周辺化してデータを表現するからです。この場合、P(H)はそれぞれの仮説に対する信頼度のような事前知識を表します。

*4:ちなみに機械学習界隈では、訓練データをモデルに食わせることを「学習」と呼び、未観測の値に対して何らかの予測推定を行うことを「推論」と呼ぶこともあるようでうす。しかし、ベイズ学習においてはパラメータの学習にしろ未来値の予測にしろ欠損値の補間にしろ、すべて「未観測値に対する条件付き分布の推論」で言葉は片付いてしまいます。