ベイズ学習の勉強に参考になる資料
おつかれさまです.今回はタイトルの通り,ベイズ学習を勉強する上で参考になる教科書やウェブの資料,論文等を紹介したいと思います.
ベイズ学習は確率推論に基づいた機械学習アルゴリズムの構築論です.ベイズ学習を使えば,あらゆる形式のデータに対して,未観測値の予測や隠れた構造を発見するための統一的なアプローチをとることができるため,特に現代の機械学習アルゴリズムを深く理解し使いこなすためには必須の方法論になっています.
1, ベイズ学習の位置づけ
まず,データサイエンスにおける他の方法論と,ベイズ学習の位置づけを簡単に俯瞰したいと思います.
僕の知る限り,ベイズ学習は1990年代ごろから登場してきた機械学習の方法論で,既存の学習アルゴリズムを確率モデルによって構築し,学習や予測の計算をすべて確率推論(条件付き分布と周辺分布の計算)で解決してしまおうという試みによってはじまりました.これにより,従来の学習アルゴリズムの問題点だった過学習,次元の呪いなどをうまく解決できる(あるいは,問題ですらなかった)ことがわかりました.また,既存の手法がベイズ学習の極めて特別な場合であるとして再定義出来ることが多く,k-means,サポートベクターマシン,ニューラルネットワーク,主成分分析などなど,数え上げればキリがないですが,これらはすべて確率モデルとして再構築でき,従来の学習方法のほとんどは対応する確率モデルに対する特別な近似推論であることが示せます.
ちなみに,最近では深層学習の各種の問題点(大量のデータを必要とする,過学習する,不確実性をハンドル出来ない,ニセのデータに騙される)などをベイズ学習の手法でエレガントに解決する方法が提案され始めているほか,深層学習の各種の計算テクニック(ドロップアウトなど)も実はベイズ学習の近似推論計算であったりすることが発見されています.また,次の動画が参考になりますが,深層学習はベイジアンの目からは「高次元データの多層構造による表現を学習する方法」とされており,グラフィカルモデル*1で表現可能なモデルの一つであるという認識になっています.
さて,すべての未知の値の予測を確率計算のみで行ってしまおうというのがいわゆるベイズ主義とされていますが*2,その反対は頻度主義と呼ばれているようです.したがって,データ解析の分野を俯瞰すれば,「頻度主義 or ベイズ主義」×「統計学 or 機械学習」の組み合わせでおおよそコミュニティが分類できるようです*3.統計学と機械学習の違いは微妙ですが,機械学習の場合は画像や音声などを含めたより複雑な構造のデータを解析対象にする傾向があり,それに伴ってコンピュータを使った効率的な計算の実行に焦点が置かれているようです.頻度主義,ベイズ主義の違いをここでは深入りして説明することはしませんが,もし興味があれば次の動画が参考になると思います.
次にベイズ学習に関連する資料をいくつか挙げていきますが,参考書(PRMLとか)によってはベイズ主義と頻度主義がごちゃごちゃに混ざっている場合があるので,内容を理解するためには十分注意した方が良いでしょう.
2, ベイズ学習を勉強するためのお勧め資料
前置きが長くなってしまいましたが,ここでは主にベイズ学習(ベイズ主義機械学習)を勉強する際に参考になる資料を紹介します.
・PRML
Pattern Recognition and Machine Learning | Christopher Bishop | Springer
Chris Bishopによるベイズ学習の決定版の教科書です.とはいえ,機械学習全体をある程度俯瞰するためにも作られたためか,ベイズではない手法も半分くらい混じっています.次に挙げる章が特に重要です.
- 1,2章の確率計算に関する基本
- 3,4章の回帰・識別の基本
- 8章のグラフィカルモデル
- 9章の混合モデル
- 10,11章の近似推論・サンプリング手法
10章の変分推論が理解できれば,12,13章の各種潜在変数モデルを参考にするよりも,後述のBealの博士論文の方が良いと思います.また,ガウス過程(カーネル)の話もRasmussenのテキストの方が詳しいです.
・BDA
Home page for the book, "Bayesian Data Analysis"
Andrew Gelmanらによるベイズ統計の定番書籍です.統計学の本ですが,各種の確率分布の使い方が解説されているのはもちろん,後半の章では次のような機械学習に深く関連する話題がたくさんあります.
・Machine Learning: A Probabilistic Perspective
Machine Learning | The MIT Press
Kevin Murphyによる,現在出版されている中でも最も網羅的な機械学習の解説書です.ページ数が1000を越えているので,これを使って勉強しようっていう人はあんまりいないと思います.リファレンス的に使うのが良く,僕も崩壊型ギブスサンプリングの解説記事を書くときとかはこの本を参考にしました.
・BRML
David Barber : Brml - Home Page browse
Bayesian Reasoning and Machine Learningの略です.なぜかウェブでフルバージョンのPDFがダウンロード出来ます.
・GPML
Gaussian Processes for Machine Learning: Book webpage
Carl Edward Rasmussenらによるガウス過程の解説書です.
・The Matrix Cookbook
ベイズとは直接関係ないですが,行列の展開や微分計算などの便利な公式がたくさん載っています.
・Variational Algorithms for Approximate Bayesian Inference
Matthew J. Beal - Thesis: Matthew J. Beal, Variational Algorithms for Approximate Bayesian Inference
隠れマルコフモデル等に対する変分推論や初期の平均場近似の使い方の解説記事として良くまとまっています.
・Introduction to Probabilistic Topic Models
http://menome.com/wp/wp-content/uploads/2014/12/Blei2011.pdf
トピックモデルのみの短い解説記事ですが,実際の課題に対してどのように確率モデルを構築・拡張するのか簡単に俯瞰できる内容になっています.
・Nonparametric Bayes Tutorial
http://stat.columbia.edu/~porbanz/npb-tutorial.html
ベイジアンノンパラメトリクスに関する解説記事・論文が網羅されています.
・Probabilistic Modelling and Bayesian Inference
http://mlss.tuebingen.mpg.de/2013/2013/Ghahramani_slides1.pdf
ベイズ学習の解説スライドで,基本的な思想や利点などが説明されています.
まとめ
以上の教科書や解説記事は,それぞれの分野のパイオニアたちが執筆した極めて品質の高い資料であるため,アルゴリズムを開発したり調べ物をする際にはとても参考になると思います.他にも秀逸な記事がありましたらご提案いただけたらと思います.
ただし,ここまで色々挙げといてあれですが,最も大事なことはここで挙げた教科書等を100%完璧に理解してやろうなどと思わないことです.正直なところ,僕も紹介した参考文献の10%~20%くらいしかちゃんと読んでいない気がします.最も効率的なやり方は,業務や研究活動で実際に直面している課題に合わせて,基礎内容の勉強,応用事例の調査,実装と動作の確認をバランス良く繰り返していくことです.そのような実務的なプロセスを通すことによって,アルゴリズム開発者の抱える多くの「○○○がしたい!」にとことん応えてくれるベイズ学習の包容力に気づかされることになると思います.
日本語で書かれた参考文献がほしい!という方には,次のような入門書もあります.
実践!ベイズ学習
今回は、実問題を解くためのベイズ学習による機械学習アルゴリズムの構築方法に関してざっくり俯瞰してみたいと思います。ここで解説するフローは僕が実問題にアプローチする際に意識しているものですが、おそらくこれはベイズ学習のみならず、広く一般的な統計モデリングや機械学習の問題解決にも適用できると思います。
<アルゴリズムの開発フロー>
 あまりファンシーな図でなくて申し訳ないですが、これから1つ1つの項目と各々の遷移に関して説明していきます。
あまりファンシーな図でなくて申し訳ないですが、これから1つ1つの項目と各々の遷移に関して説明していきます。
1、データ・課題の整理をする
まず、機械学習を使って解きたい問題や実現したいサービスを定義してみます。データはあるんだけど何をして良いかわからない、という場合もあるかもしれませんが、そういうときでもとりあえず何かしらの目標を仮置きしてみるのが良いかと思います。基本的に機械学習でできることは「見えない情報の予測」であると考えればアイデアが発想しやすいかもしれません。未来の株価の予測、画像や音声の判別、欠損データの補間、異常値の特定など、これらはすべて未知の事象に対する予測問題として定義することができます。*1
課題が決まれば、次第に必要なデータは明らかになってきます。例えば、明日の東京都全体の電力需要を予測したいのであれば、過去の需要データに加え、その日の天気や曜日の情報(平日or休日)なども予測に役に立つでしょうし、その日に起こる予定のイベントとかも考慮しておいた方が良いかもしれません。この辺りはデータの収集コストと相談する必要もあるかと思います。また、データそのものの収集に伴って、データに関する周辺的な知識(よく知られた法則、物理的な制約など)も色々仕入れておけば、後のモデル構築の段階に役立てられる可能性が高いです。
また、集めたデータの形式や粒度がバラバラだったりする場合はこの時点で揃えておくのが良いかもしれません。ただし、欠損値の補間や異常値の除去、データサイズの補正などのいわゆる「前処理」をここで行ってしまうと、後段のアルゴリズムに対する情報欠損に繋がる可能性があります。手間とコストを十分に考慮する必要がありますが、理想的には、これらの処理はモデルと推論(2および3)で行う方が良いです。
2、モデルを構築する

ここでは確率モデルP(X, Θ)の構築を行います(Xがデータで、Θが学習したいパラメータなどの未観測変数)。基本的なアプローチとしては、「今手元にあるデータXは一体どういうプロセスを経て生成されたのか?*2」ということを念頭に置き、基本的な確率分布を組み合わせてモデルを構築します。
持っているデータの種類によってもモデル構築の仕方が大きく変わってきます。例えばラベルデータを十分に持っているのであれば、既存の教師ありの識別モデル(線形回帰、ロジスティック回帰、ガウス過程など)をそのまま使うのでも良いかもしれません。*3
最も大事なことは、この段階でデータをよく観察し、普遍的な性質や特徴を整理することです。そのような知見をどれだけモデルに組み込むことが出来るかが、未知の値を予測するにあたって非常に重要になってきます。ちなみに、生データに対して何かしらの特徴量抽出を行うやり方も手軽ですが、このような段階を踏んだ情報処理の過程にしてしまうと、その都度情報欠損が起きてしまう可能性があることに注意してください。これを防ぐには、特徴量抽出のプロセスも確率モデルとして組み込むのが理想的です。
さらに、確率モデルを構築した後に必ずやってほしいことは、モデルP(X, Θ)から仮想的にデータXをサンプル(シミュレート)してみることです。このサンプルが、我々が実データを学習させる前に持っている「仮説」を具体的に表していることになります。例えば、データXとして成人男性の身長を仮定しているのに、モデルからサンプルしてみた値が0 cm近辺にへばりついたちっさい値しか出てこないとかいう場合は、明らかにモデル自体か事前分布の設定等が誤っています。モデルからのサンプルが実際に発生し得るデータをちゃんとカバーできそうかどうか、次の推論導出に進む前にチェックしておくのが大事です(「作ったモデルでもっと遊んでね」と僕は表現します)。
3、事後分布を計算する(推論を実行する)
前ステップで構築したモデルをもとに、事後分布P(Θ|X)を評価します。
伝統的な確率推論に対して、機械学習を機械学習たらしめているのはおそらく取り扱う確率モデルの複雑さにあると思います。多くの問題では事後分布が解析的に得られず、推論アルゴリズムを導いてコンピュータ上で実行することになります。具体的にはMCMCや変分近似などの近似推論アルゴリズムを導出してPythonやJulia等の適当な言語で実装するほか、モデルがそれほど複雑でないのであればStanなどのツールを使って自動的に推論してもらうという手もあります。
また、多くの機械学習の課題では、ただパラメータの事後分布を計算するだけを目標とするということはあまりないでしょう。例えば未来の値X*を予測したい場合は、学習された事後分布を使って予測分布P(X*|X)=ΣP(X*, Θ|X)を評価することになると思います。あるいは、クラスタリングなどの「観測することのできない潜在的な値を推定する」問題では、潜在変数モデルP(X,Z,Θ)に対する潜在変数の事後分布P(Z|X)を計算することになります。
ところで、このステップでは多くのバグに苦しむことになります。手で導出した推論アルゴリズムがきちんと動作しているか確認する方法はいくつかあり、一番のオススメとしては、いきなり実データに挑戦せずに、学習前のモデルから仮想的にサンプルしたデータを改めて訓練データとして使って推論させてみることです。このようにすればデータに対するモデルは100%正しいことが保証されるので、推論アルゴリズムの導出式や実装のバグのチェックのみに集中することできます。また他には、例えば変分ベイズ法などの特定の方法では、変分下限と呼ばれる値を評価することにより(ある程度は)動作の正当性を確認できます。
モデル構築および近似推論に関する関連記事は例えば次のようなものがあります。
グラフィカルモデルによる確率モデル設計の基本 - 作って遊ぶ機械学習。
ベイズ混合モデルにおける近似推論① ~変分近似~ - 作って遊ぶ機械学習。
4、結果の評価を行う

作ったアルゴリズムが所望の動作を実現しているか、あるいは改良がうまくいっているかを評価します。モデル自体を評価するような指標(周辺尤度、BIC、AICなど)もありますが、基本的には今解いている課題に即した評価手法を使うのが自然かと思います。例えば連続値の予測であれば二乗誤差で評価するのが(ベストかどうかはともかく)簡単ですし、低頻度のイベントを検知するような課題であればF値を使うのが良いかもしれません。ただし、結果の1%や2%を競うような数値評価至上主義*4に陥らないように注意してください。また、見落としがちではありますが、実際のところ機械学習を使ったサービスなどでは視覚的に結果の良し悪しを確認したり、自分でサービスを使ってみて感触を確かめる、というのも重要な評価手段の1つになります。
それに伴って、アルゴリズムの計算効率(メモリ量や計算速度など)も合わせて評価するのが重要です。というのも、最適化やサンプリングに基づく多くの機械学習アルゴリズムは、時間をかければかけるほど最終的な性能が高くなるものが多く、計算コストを無視した推定精度のみの評価はほとんどの場合では不十分になるためです。
また、機械学習の課題で訓練データとテストデータを分けて評価するのは必須だと思われます(クロスバリデーションなど)。これは過学習をしていないかチェックするための超基本手段なのですが、意外にちゃんとやっていない人が多くてびっくりです。ちなみに「ベイズ学習はそもそも過学習をしないので、データを分けなくても評価できる」という主張もありますが、現実的に多くの場合では近似アルゴリズムを推論に使うことになるので、オーバーフィットやアンダーフィットに近しい現象も起こり得ます。なるべく本番環境に近い状態で評価するためには、やはりテストデータに対する課題依存の評価指標を設定するのが無難かと思います。
確率モデルを使った機械学習アルゴリズムでは、得られた事後分布から仮想的にデータをサンプルしてみるのも学習がうまくいったか直観的にチェックするポイントになります。例えば、顔画像Xを学習する問題を考えてみましょう。事前分布P(Θ)をもとにP(X|Θ)からデータをサンプルしてみると初めはぐちゃぐちゃなノイズしか出てこなかったのが、学習された事後分布P(Θ|X)をもとにサンプルした場合は「顔っぽい」データがちゃんと生成できるようになっているはずです。これがうまくいかない場合は、モデルの表現能力に問題があるか、訓練データ数が少ないか、あるいは推論アルゴリズムの性能が十分でない可能性があります。
よく起こる遷移
・推論導出からモデルの再構築(3→2)
2で構築したモデルが奇怪すぎて推論アルゴリズムがうまく導けない場合があります。
それでも無理やり追加の近似などを仮定してアルゴリズムをひねり出すこともできますが、多くの場合は性能がよくなりません。モデルの構築と推論の導出は分けられたプロセスとして認識すべきですが、実際は相互に行き来しながら一番良い組み合わせを探していくことになります。
・性能評価から推論の再導出(4→3)
アルゴリズムの導出はうまくいっているはずなのに、実データに対して思うような性能が出ない場合は、推論アルゴリズムを再検討してみる必要があります。具体的には、必要メモリ数があまりにも多すぎた場合などは、学習アルゴリズムをオンライン化(Stochastic Gradient Descentなど)してデータを小分けに出来るようにするなどが考えられます。他にも、例えばMCMCが遅すぎる場合は変分近似を使ってみる方が良いかもしれません。
・性能評価からモデルの再構築(4→2)
実験結果を眺めることにより、「うまくモデル化できていない特徴」というのが見えてくる場合があります。この場合は2に戻って、新しい特徴をモデルに組み込むことが必要になってきます。例えば、データに明らかに時間的依存性があることがわかった場合は、モデルをマルコフモデルにするなどの手段が考えられます。
逆に、作ったモデルが複雑すぎるために推論アルゴリズムの性能が出ていない可能性もあります。こういう場合は、ちょっと悔しいですが、モデルから余計な要素を切り落としてシンプル化するのもアリなんじゃないかと思います。
・性能評価から課題の再設定(4→1)
評価結果が思わしくない場合は、データの量や質に関する問題に着目するか、あるいは課題自体を検討しなおしてみるのが良いかもしれません。実際、4の段階にまで入ると、データに関する知識やアルゴリズムの計算コストなども最初の頃よりだいぶ頭に入ってきているはずなので、実運用に基づいた課題の再設定などは積極的に検討すべきなのではないかと思います。
- - -
以上、思いつくままにバァーッと書いてしまいましたが、少しでもベイズ学習あるいは確率モデルによる機械学習構築を検討される際に参考になればと思います。
今回の記事がよくわからん!という方には,次のような入門書もあります.
*1:他にもデータの圧縮、ノイズの除去なども確率モデルの得意とするところです。
*2:いやいや、深層学習とか認識系の課題であれば「データがどういうプロセスを経て認識されたのか」の方が正しいでしょ、とおっしゃる方もいるかもしれません。その場合は、人間が与えるラベルデータが「どのような認識的な処理過程を経て生成されたのか」をモデル化する、と考えれば、文中の言い方でも悪くない気がします。
*3:ところで「教師あり」というのはつまり、「予測したい値と同質と思われるデータを学習用に持っている」とした場合の機械学習の実装方法だと解釈できます。つまり、解きたい実課題自体が教師ありだとか教師なしだとか言うのはナンセンスで、アルゴリズムを開発する人間がその課題をどう捉えるかに依る、というのが正しいと思います。
*4:定量評価というものは、実現したい目標を理解しやすく数値に要約したもの、あるいは仮置きしたものに過ぎません。よっぽど単純な問題でない限り、絶対的な数値評価指標などというものは存在しないと思った方が良いです。
機械学習の4つのアプローチ
おつかれさまです。今日はちょっと趣を変えて、近年のいわゆる「機械学習」という技術のアプローチをカジュアルに少しカテゴリ分けしたいと思います。
といっても、自分はアカデミックの研究者ではなく大量の論文を読み漁るということもほとんどしないので、理論的なバックグラウンドに基づいたソリッドなカテゴリ分けはできません。ここで紹介するのはあくまで、実用上の機械学習技術者から見た視点で「こんな傾向があるかなぁ」くらいの気持ちで書いたものです。
<代表的な4つのアプローチ>
1、最適化(目的関数ベース)
まず始めは最適化手法をベースにした機械学習のアルゴリズムです。たぶん一番例が多いんじゃないでしょうか。
ここでは、ある解きたい課題を目的関数によって定式化し、適切な最適化手法を使って解きます。伝統的な線形回帰や線形識別はもちろん、主成分分析(PCA)や非負行列因子分解(NMF)なんかもこの枠組みで解かれることが多く、ほとんどの場合で誤差関数を定義してそれを最小化するというアプローチを取ります。他にはサポートベクターマシン(SVM)なんかもマージン最大化という基準にしたがって最適化を行いますね。
この種のアルゴリズムの利点としては、比較的自由に目的関数をデザインして解くことができる点が挙げられると思います。
欠点としては、ある種の複雑な課題に対してはそもそもどうやって目的関数を設定していいかわからない場合があることと、最適化に基づいているので簡単にデータに対してオーバーフィットしてしまうことです。また、予測が「どれだけ確からしいのか」といった、予測に関する不確実性・信頼性に関する情報を上手く扱えないことが多いです。
2、深層学習
最近流行っているあれです。一番シンプルな例は(伝統的な)ニューラルネットワークなどで、アイデアとしては、データの表現を多層構造を使って学習することにより、データの次元間にまたがった共通の特徴を高レベルの層でシェアして汎化性能を高めようというものです。画像や音声の認識タスクで性能を発揮するようです。
利点としては、概念が比較的わかりやすいこと、ある特定の課題に対して顕著な性能を発揮していることです。
欠点としては、基本的にものすごい量のデータと計算コストを使用しなければならないことと、アルゴリズムのパフォーマンス向上(モデル設計やチューニング)に系統だった手段がないことです。あと、だいたい単純な誤差関数の最小化とかを基準にするので上の方法と同様オーバーフィットしやすいです。あとは、現状あまり理論面が洗練されていないのも課題です。
3、機械学習ライブラリ
これもカテゴリに入れていいのか謎ですが、実際の現場ではよく使われています。Scikit-learn*1などの機械学習ライブラリを駆使して問題を解くという、あらゆる場面で比較的にスピーディーに試せる方法です。
基本的なアプローチとしては、入力データをよく眺めて、特徴量抽出や次元削減などを行い、その結果を識別器にかけるというものです。
利点としては、ややこしい数学の知識などがなくてもプログラミングさえ少しできれば誰でも始められることです。機械学習の入門として、あるいはクイックプロトタイピングとしてお勧めかもしれません。あとは、わりと洗練されたライブラリが世に出回っているので、自分でいろいろアルゴリズムを開発してバグに悩まされるという心配もあまりありません。
欠点としては、解けるタスクが非常に限られていることです。問題自体をデザインすることがほとんどできないので、最大性能もほかのアプローチと比べて限界があります。
4、ベイズ学習
すべての問題を確率モデリングと確率推論の2ステップで解くアプローチです。
基本的には、データの発生プロセスを確率分布を使って物理的・論理的に記述し(モデリング)、計算機を使ったアルゴリズムによって事後分布を計算する(推論)という流れです。上に具体的に挙げたような各アルゴリズムの多くがベイズ化できるほか、ベイジアンノンパラメトリクスと呼ばれる、ガウス過程やディリクレ混合過程などといったベイズ手法ならではのモデルもあります。
このアプローチの利点としては、基本的にはオーバーフィットをしないため*2、少量・多次元のデータでも性能が出やすいことです。 また、確率分布を組み合わせてモデルを自由にデザインできるので、幅広い課題に対してアルゴリズムを与えることができます。
欠点としては、アルゴリズムの導出に多少の数学力を要することと、厳密な計算には非常に計算コストがかかることです。
<ベイズ学習の汎用性>
で、自分は完全なベイズ派なので、最後に今一度ベイズ学習の汎用性と、他の3手法との関係性について触れたいと思います。
1、ベイズ学習と最適化
ベイズ学習でも最初に挙げた最適化手法をサブルーチンとして使うことは良くあります。というのも、ある種の最適化問題は、ベイズ学習で必要となる積分の近似と等価になるからなんですね。
例えば最尤推定(最小二乗法を使った誤差関数の最小化)なんかも、実はベイズの近似推論に対して極端な仮定を置くことで導かれます*3。主成分分析、非負行列因子分解もベイズ化できるほか、サポートベクターマシンとガウス過程の関係性も指摘されています*4。
2、ベイズ学習と深層学習
ベイズ学習は汎用的なデータ解析の枠組みであるので、もちろん深層学習の多様なモデルをベイズ学習として再定式化することができます。代表的には、ガウス過程を使ったディープなモデル*5があるほか、変分ベイズを使ったオートエンコーダの実装*6もあります。あとは畳み込みニューラルネットワーク(CNN)をベイズの枠組みで焼き直して変分近似で解くといった手法とかもあります*7。
さらに,ユニット数が無限のニューラルネットワークはガウス過程と等価になります.
3、ベイズ学習とライブラリ
ベイズ学習の1つの欠点は、近似推論手法の開発に非常に数学力と手間がかかることです。この手間を省いてくれるものとして、種々の統計確率言語があります。代表的なものにはStan*8があり、モデルの記述さえすればあとは勝手に近似推論アルゴリズム(MCMCや変分推論)を実行してくれます。残念ながら、複雑なモデルに対する推論性能は現在のところあまりよろしくないようです。
他にはベイズの枠組みで作られたアルゴリズムがそのままライブラリ化されている場合ももちろんあります。最近人気なのはガウス過程を使ったベイズ的最適化(Bayesian Optimization)で、深層学習のチューニングなんかに使われているようです。
- - -
さて、ちょっとした落書きのような記事になってしまいましたが、少しでもたくさんある機械学習技術のアプローチとその関係性がクリアになっていただければ幸いです。
*1:Scikit-learn: http://scikit-learn.org/stable/
*2:PRMLとかではオーバーフィットしないと言い切ってますが、実際の多くの場面では近似アルゴリズムを使うので、近似性能が悪ければオーバーフィットもアンダーフィットも起こり得ます。
*3:最尤推定、MAP推定、ベイズ推論 - 作って遊ぶ機械学習。
*4:Gaussian Process for Machine Learning: http://www.gaussianprocess.org/gpml/
*5:Deep Gaussian Process: http://www.jmlr.org/proceedings/papers/v31/damianou13a.pdf
*6:Auto enoding variational Bayes: https://arxiv.org/abs/1312.6114
*7:Bayesian CNN: https://arxiv.org/abs/1506.02158
*8:Stan: http://mc-stan.org/
ベイズ推論による機械学習の基本
今回は基本的なベイズ学習の概念と流れを説明したいと思います。まず始めに、ベイズ学習のすべての基本となる2つの計算規則(和の規則、積の規則)を取り上げます。また、ベイズ学習に関わるややこしい用語たち(データ、尤度関数、事前分布、事後分布、エビデンス、予測分布、などなど)に関しても念のためここで整理しておきたいと思います。そして最後に、簡単な多次元のガウス分布とウィシャート分布を使ったベイズ推論の例を取り上げ、それぞれの用語や概念との具体的な結びつきについて触れたいと思っています。
・ベイズ学習の基本概念
さて、確率モデルを使ったベイズ推論を行う上で最小限必要なのは次のたった2つの計算ルールです。
<和の規則>
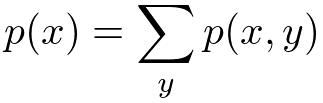
<積の規則>
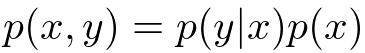
は同時分布(joint distribution)、
は条件付き分布(conditional distribution)と呼ぶんでした。極端な言い方をしてしまうと、ベイズ推論による機械学習のすべては、この2つのルールをいかに効率よく用いることによって未知の確率分布を計算するかということに尽きてしまいます。
さて、もう少し踏み込んでみましょう。まず最初に、上の2つの規則を組み合わせることによって次のような有名なベイズの定理(Bayes's theorem)を得ることができます。
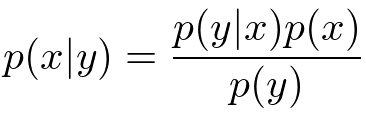
で表される確率分布を、逆にした
やその他の項の組み合わせで表現できてしまうというのがこの式の言わんとすることです。このことから、ベイズ推論は逆確率の法則なんて呼ばれたりもするみたいです。
ここでようやく機械学習らしい概念を導入してみることにします。といってもちょっと用語を導入してみるだけです。の代わりに
を、
の代わりに
を文字として用いると、ベイズの定理は次のようになります。
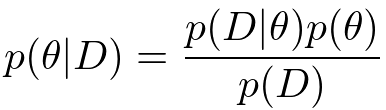
ここではデータ、
はパラメータと呼ぶことにします。
さて、データに関しては説明は要らないでしょう。写真データとか、人の声の録音データとか、月間の製品の売り上げデータとかなんでも想像しやすいものでOKです。データは複数そろっていることを基本的には想定しますが、実は1個でも0個でも大丈夫だったりします。
は一般的にはパラメータと呼ばれます。 ベイズ学習においてパラメータは推論すべき未知の変数として扱われます*1。
さて、改めてこの重要な式をじっくり見てみることにしましょう。まずは尤度関数(likelihood function)と呼ばれています。パラメータがある特定の値に条件づけされたときに、データ
がどれだけモデルから発生しやすいかを表現しています。その後ろについている
は事前分布(prior distribution)と呼ばれており、
の分布に関する我々の事前の仮説(どんな
が出やすいのか?)を表現しています*2。それに対して一番左の式
は事後分布(posterior distribution)と呼ばれています。こちらも事前分布と同様パラメータの不確かさを表す確率分布ですが、データ
によって条件づけされているところが違いますね。この分布は尤度関数を通すことによって更新された
の分布というふうに解釈することができます。ベイズ学習の主要な課題はこの事後分布をいかに効率よく、精度高く計算するかにあります。
さて、尤度関数と事前分布の掛け算をしただけでは事後分布の計算は完了しません。分母にもう1つ項がついていますね。これはエビデンス(evidence)あるいは周辺尤度(marginal likelihood)呼ばれており、事後確率がちゃんと正規化される(=分布を積分すると1になる)ことを保証するために必要になってくる項です。エビデンスは和の規則を用いることによって次のように計算することができます。
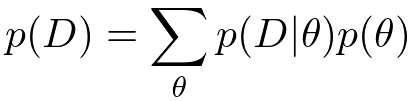
「分子の項における
を和の規則で除去しなさい」と言っているんですね。簡単なガウス分布などを使ったモデルであればこの項は解析的に計算できるのですが、少し複雑なモデルになってくるとこの和が計算できなくなってしまいます。離散の場合は組み合わせ爆発を起こし、連続の場合には積分が解析不可能になってしまいます。ちなみにこのモデルエビデンスの値を使って複数のモデルの良し悪しを直接決めることもあるようです(モデル選択*3)。
さて、最後にもう1つ大事な概念を紹介してみましょう。機械学習では、ある学習データを使ってモデルを訓練させ、新しいデータに対して予測を行う、というのが代表的なアプリケーションになります。したがって、次のような新しいデータに関する予測分布(predictive distribution)を計算することも重要な課題の1つです。
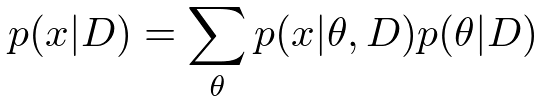
事後分布(学習済みのパラメータの分布)を使って、まだ入ってきていない新データに関する確率分布(平均とか分散とか)を計算しようというわけです。
ここまでのベイズ学習における基本的な流れをまとめてみると次のようになります。*4
1、尤度関数(観測データの表現方法)を定義する。
2、事前分布(パラメータの散らばり具合)を設定する。
3、ベイズの定理を使って事後分布を更新する。(=学習)
4、事後分布から予測分布を計算し、未知の値の確率分布を求める。(=予測)
・ガウス分布とウィシャート分布を使った具体例
ちょっと抽象的な話が続いてしまったので、次は具体的なモデルの例を当てはめて話を進めたいと思います。今回は、D次元、N個の観測データをとおくことにします。尤度関数と事前分布は具体的には次のように定義してみたいと思います。
<尤度関数(ガウス分布)>
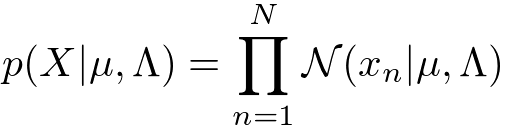
<事前分布(ガウス・ウィシャート分布)>
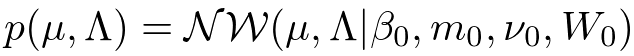
ガウス分布(Gauss distribution)はデータに対するノイズを表現する上で最も一般的に使われているモデルの1つです。ガウス分布には2つのパラメータ(平均)と
(精度行列)がありますが、ベイズ学習ではこれらは確率変数として扱われます。したがって確率分布が必要になってくるのですが、今回は計算が解析的になるという理由で共役事前分布(conjugate prior distribution)のガウス・ウィシャート分布(Gauss-Wishart distribution)を用いることにします。ちなみに
、
、
、
といった文字は超パラメータ(hyper parameter)と呼ばれており、事前分布の形状を決定するものになります。これらは確率変数として扱われず、固定された値を持ちます。
さて、ここまでが準備段階です。次にこのモデルを使ってデータを「学習」してみたいと思います。もっと丁寧に言うと、ベイズ学習における「学習」とは、データを観測した後の、パラメータの事後分布
を計算することに対応します。今は非常に基本的なガウスモデルを使っているので、特に最適化やサンプリングなど凝ったテクニックは必要とせずに解析的に手計算することができ、得られる分布は事前分布と同じ形状(ガウス・ウィシャート分布)を持ったものになります。
具体的には、次のようにベイズの定理の分子だけを使ってと
の関数を求めてあげると、いくらか計算が楽です。
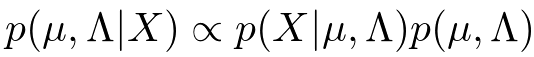
得られた式を正規化してあげることにより、ガウス・ウィシャート分布が得られれます。
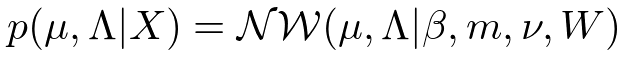
分布の形状を決めるそれぞれの超パラメータは事後分布では次のような計算結果になります。
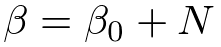
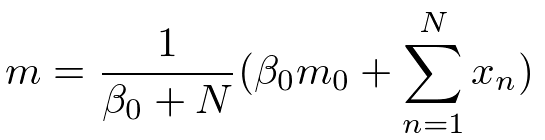
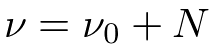
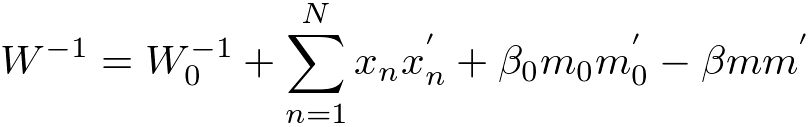
計算過程は省きましたが、このような結果が自分ですらすら計算できるようになるとベイズ学習の入門コース卒業になります。
それでは次に予測分布も求めてみましょう。一般的にはパラメータの分布を学習しただけで満足するケースはあまりなく、学習後のモデルを使って何らかの予測を行うことが機械学習における主要なテーマになってきます。
さて、予測分布の計算は未観測のデータに対する尤度関数と事後分布を掛け合わせ、パラメータだけを積分除去すれば得られるんでした。さっそく計算してみましょう。
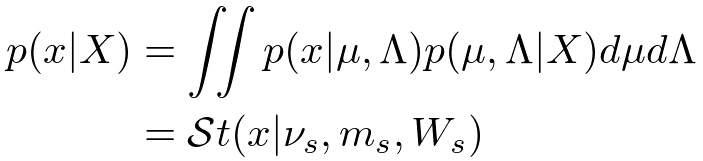
ガウス分布の平均パラメータと精度パラメータを両方とも積分除去しなければならないので若干計算がめんどくさいですが、結果は解析的に計算でき、スチューデントのt分布(Student's t-distribution)が得られます。それぞれの超パラメータは次のようになります。
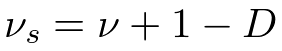
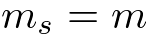
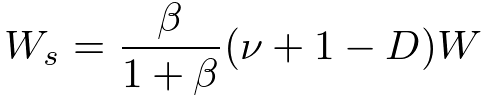
・まとめ
今回はベイズ推論を使った機械学習の基本的な流れに関して説明しました。単純な線形回帰モデルなんかは今日の結果を利用すれば比較的簡単に構築することができます。一方で線形識別(ロジスティック回帰など)は前述の積分計算が解析的に実行することができず、ラプラス近似などの近似手法を使う必要があります。またクラスタリング等で使われる混合モデルや時系列データを取り扱うためのHMMなんかも、一般的には解析計算ができないので変分近似やサンプリングなどの近似手法に頼ることになります。ただこれらは単に計算上の問題なので、基本的には上述のベイズの定理を使った学習の枠組みを使って事後分布を計算するという流れは変わりません。
今回の記事がよくわからん!という方には,次のような入門書もあります.
*1: ”パラメータ”という用語はなんだか固定された値のように聞こえてしまうことがあります。最近では今回の記事のようなを(すべてのデータ点に共有される確率変数という意味で)”大域確率変数(global variable)”と呼んだりすることもあるようです。
*2:事前分布は基本的にデータを観測する前に決めてあげなければいけません。具体的にどのような事前分布を選んだらいいのかは、また別の機会でお話しします。
*3:ちなみに究極のベイジアンはモデル選択すらしません。仮説(あるいはモデル)Hが複数個あった場合、P(X) = ΣP(X|H)P(H)のようにすべての仮説を周辺化してデータを表現するからです。この場合、P(H)はそれぞれの仮説に対する信頼度のような事前知識を表します。
*4:ちなみに機械学習界隈では、訓練データをモデルに食わせることを「学習」と呼び、未観測の値に対して何らかの予測推定を行うことを「推論」と呼ぶこともあるようでうす。しかし、ベイズ学習においてはパラメータの学習にしろ未来値の予測にしろ欠損値の補間にしろ、すべて「未観測値に対する条件付き分布の推論」で言葉は片付いてしまいます。
ややこしい離散分布に関するまとめ
今回は離散分布(discrete distribution)の代表格である多項分布(multinomial distribution)や、その共役事前分布であるディリクレ分布(Dirichlet distribution)との関係性や計算方法を整理したいと思います。
離散分布というと、本来はポアソン分布(Poisson distribution)なども含めた離散値を出力するような分布全般のこと指します。しかし実際に論文などを読んでいると、くじ引きのように単純に出目の比率が与えられたような分布を離散分布と名付けてしまっている場合もよく見られます。まぁ文脈的に誤解を招くことはあまりないと思うのですが、くじ引きの分布をもっとキッチリ表現するなら、複数あるカテゴリーから1つを抽出するという意味でカテゴリカル分布(categorical distribution)と呼ぶのが適切かと思います。あるいは、観測回数が1の場合の多項分布とかって呼ぶこともできますね。
とまぁ別に名前はどうでもいいのですが、これらの離散分布の関係性をまとめてみると次の図のようになります。

ピンクの線が多次元変数への一般化で、オレンジの線が複数回の試行を行った場合に対する一般化です。グレーの点線矢印は、それぞれの確率分布に対する共役の関係性を示しています(矢印の元に当たるのが共役事前分布(conjugate prior)です)。
結論としては、多項分布とその共役事前分布であるディリクレ分布の計算だけある程度馴染んでおけば、後はその特殊な例なのでいちいち気にする必要はないということになりますね。
<各確率分布の自己紹介>
さて、これからいろいろ計算確認をする前に、それぞれの確率分布の定義式を列挙してみます。
・ベルヌーイ分布(Bernoulli)

お馴染みのひしゃげたコインの分布です。は0か1のどちらかの値を必ず取り、パラメータは
をみたします。*1
・二項分布(Binomial)
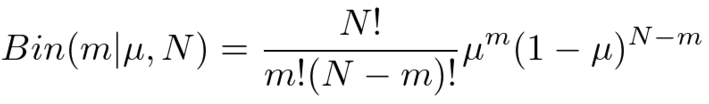
コイントスを回行った時の、表面の回数に関する分布です。したがって
は0以上
以下の整数値を取ります。ベルヌーイ分布と同様、
です。
・カテゴリカル分布(Categorical)

こちらもお馴染みの面を持つひしゃげたサイコロの分布ですね。
次元ベクトルである
の要素
は0か1のどちらかの値を必ず取り、いずれか1つの
しか1にならないので、
をみたします。それぞれの出目の確率は
で与えられ、
をみたすように設定します。
・多項分布(Multinomial)
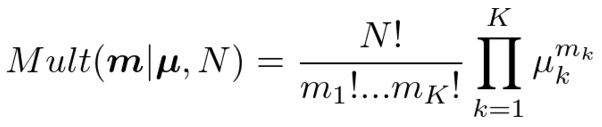
面を持つひしゃげたサイコロを
回投げた時の、出目の回数に関する分布です。したがって
次元ベクトルである
の要素
は非負の整数値を必ず取り、
をみたします。カテゴリカル分布と同様
です。
・ベータ分布(Beta)

コイントスの共役事前分布に当たる分布です。コインの「ひしゃげ具合」に関する分布になります。この分布から出てくる値は過ならず0と1の間に収まってくれるように作られています。分布の特徴を決める
や
は、0より大きい実数値を設定する必要があります。ちなみに正規化項に当たる部分にはイカつい格好のガンマ関数(gamma function)
の塊がいます。ガンマ関数は階乗「!」の実数値バージョンですが、これはライブラリとか使えば簡単に計算できるのであまり怖がる必要はないです。*2
・ディリクレ分布(Dirichlet)

サイコロの共役事前分布に当たる分布です。サイコロの「ひしゃげ具合」に関する分布ですが、混合モデル(mixture model)に使われるほか、自然言語処理で使われるLDA(Latent Dirichlet Allocation)の由来にもなっていますね。出てくる値は必ずをみたしてくれるように分布が作られています。また、すべての
に対して
は0より大きい実数値を設定する必要があります。ここでもまたイカつい
の塊が先頭にありますが、多くの場合で無視して計算できるので気にしなくても大丈夫です。
<各確率分布の関係性>
さて、自己紹介が終わったところでそれぞれの分布の関係性を式で確認してみましょう。ここでは、多項分布やディリクレ分布がその他の分布の特別な場合であることを確認してみます。
・多項分布=>カテゴリカル分布
多項分布において>と設定してあげれば、
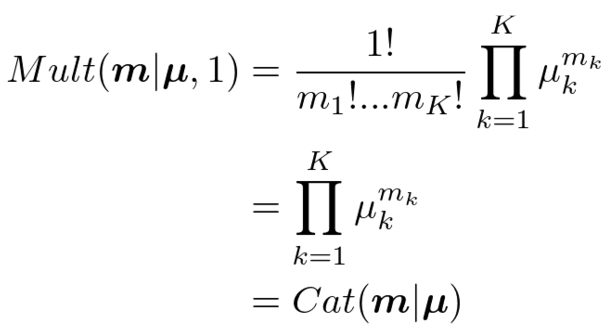
となり、カテゴリカル分布に一致します。と設定したことにより
は0か1かしか取らなくなったことと、
の計算に注意してください。
・多項分布=>二項分布
多項分布において次元をと設定してあげれば、
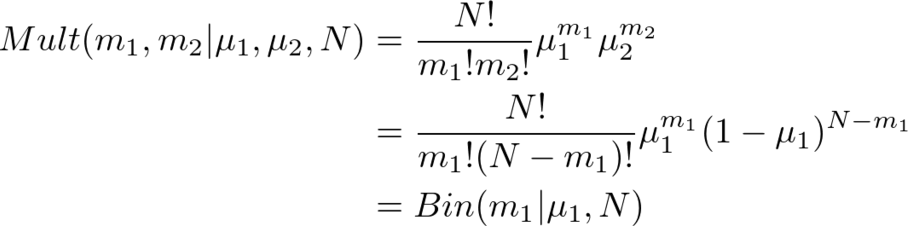
となり、二項分布になります。の制約があるので、実質
のみの確率分布になるのがポイントです。パラメータもわざわざ2個持つ必要はなく、
を考慮すれば
だけ持っておけば大丈夫ですね。
・ディリクレ分布=>ベータ分布
ディリクレ分布において次元をと設定してあげれば、

となり、ベータ分布になります。ここでも、の制約条件を利用することによって実質
のみの確率分布にすることができます。
同様に、ベルヌーイ分布はカテゴリカル分布からとおくか、二項分布から
とおくと導けます。簡単なので省略します。
<共役事前分布とベイズ推論>
さて最後に、ディリクレ分布が多項分布の共役事前分布であることを確認してみましょう。共役事前分布とは、観測モデルとかけ合わせた後に同じ関数形状が出てくるような分布のことです。つまり、ベイズの定理

を適用したときに、事前分布と事後分布
が確率変数
に関して同じ形式の関数になるように
を定めるということですね。このような事前分布を選んでおくと、各種推論計算が解析的に簡単に計算できるようになるほか、データを小分けにして学習させるオンライン学習(online learning)を構築することも容易になります。オンライン学習は逐次学習(sequential learning)、追加学習(incremental learning)とも呼ばれるようです。
ということで、ディリクレ分布を事前分布とし、多項分布に従うデータを観測した後の事後分布を計算してみましょう。

正規化項(ガンマ関数とか階乗とか含んでる項)を無視して計算するのがラクする秘訣です。さて、結果の式を見てみると、ディリクレ分布と同じ関数形状をしていることがわかります。したがってとおいてあげれば、
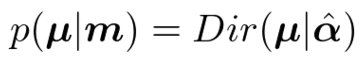
ということになり、事後分布もディリクレ分布になることがわかりました。*3
また、上のベイズ推論でと置けば、カテゴリカル分布のパラメータに関する学習も同様にディリクレ分布を使って行うことができることがわかります。これは特に混合モデル(クラスタリングなど)を扱うときに出てくる計算なので、ある程度慣れておくと便利です。
今回の記事がよくわからん!という方には,次のような入門書もあります.
第一線のAI研究者が注目する最新機械学習技術6選(NIPS2015招待講演より)
ちょっと前になりますが、昨年12月に行われた機械学習のトップカンファレンスであるNIPS2015の講演ビデオが上がっているようなのでチェックしてみました。今回ご紹介するのはケンブリッジ大学のZoubin Ghahramani教授の研究です。
同教授は今後excitingな機械学習の基礎・応用に関する取り組みとして次のような6テーマを紹介しています。
・Bayesian Nonparametrics
ベイジアンノンパラメトリクスでは、無限次元を持つモデルを仮定することにより、データ量に応じて適切なモデルを学習することができます。こういったモデルは関数上の確率分布(確率過程)を考慮することによって実現できます。代表的な例はガウス過程、中華料理店過程、インド料理過程などです(ご飯ばっかりですね)。
ガウス過程は、回帰や識別、ランキングや次元削減に使われています。またある種のニューラルネットワークがガウス過程の一例であることが1994年に示されているそうです。
・Probabilistic Programming
確率モデルを構築し、推論アルゴリズムを導き、実装をする・・・といったプロセスはものすごく時間がかかって大変です。Probabilistic programmingは確率モデル(あるいは確率的にデータを生成するプロセス)を記述するための言語で、推論はサンプリングや変分近似で勝手にやってくれます。代表的なのはBugsやStanです。
・Bayesian Optimization
日本語だと「ベイズ的最適化」の名前でコンセンサスが取れていたと思います。ガウス過程を使い未知の関数の最適値を探す手法です。未知の関数の評価にとても時間orコストがかかるような状況を仮定しており、いかに少ない評価回数で最適値を探せるかがポイントになります。
・Data Compression
シャノンの定理によると、すべての圧縮アルゴリズムは確率モデルに基づくそうです。ベイジアンノンパラメトリクスを使ったアダプティブな圧縮アルゴリズムが近年非常によい圧縮性能を出しているようです。
・Automatic Statistician
データを食わせるだけで何かしらレポートを返してくれるような野心的なアルゴリズムの話です。アイデアは非常にシンプルで、いくつかのカーネルを組み合わせて周辺尤度を評価することによって、データをうまく説明するような適切なモデルを探索します。
・Rational Allocation of Computational Resources
大量のデータと複数のモデルがある中、リソース(時間、CPU、メモリ、ディスクサイズ)が限られた状況下でいかに最適な機械学習システムを構築するか、という課題設定です。これを不確実性がある中での逐次的な意思決定問題として扱います。
・個人的な雑感
Bayesian nonparametricsは従来のベイズ学習に対する正当な拡張であるため、今後も基礎的な研究は発展していくかと思います。そろそろ大きなアプリケーションがほしいところですが、ディープラーニングなどの成功しているモデルもかなりの部分はこれに置き換わり、より洗練されたアルゴリズムになるのではないかと予測しています。
Probabilistic programmingは基本的に推論性能はあまりよくないようです。僕は使ったことがないのですが、とりあえず複数のモデルを素早く試したいときなんかには便利だと思います。普通にモデル構築→アルゴリズム導出→実装ってやってるとそれだけで1日使いますからね・・・。
ベイズ的最適化は非常に概念もわかりやすく応用先も広いのでぜひ多くの人に使っていただきたいと思います。日本の京などのでっかいコンピュータで何かシミュレーションを行う場合は、Bayesian optimizationで全体を包んであげると解探索が早くなるかもしれません。あまりいないと思いますが、例えば遺伝的アルゴリズムとかを使っている人は早々にこちらへの置き換えを検討した方が良いと思います。
データ圧縮も面白い領域です。結局のところ、jpegに代表されるように、非可逆圧縮というのはデータの中の捨ててもいい情報と残さなきゃいけない情報をうまく見つけることが基本になっています。これは機械学習における特徴量抽出といっしょです。画像だったら、人間が認知に必要でない情報は捨ててもいい可能性が高いと言えるわけですね。データ圧縮もかなりドメイン依存が強いかと思いますが、汎用的なアルゴリズムでどこまでいけるのかは興味深いですね。 (追記:すみません、招待講演の内容では「非可逆圧縮」ではなく、情報損失のない「可逆圧縮」の話だったようです。データに関する分布をベイジアンノンパラメトリクスを使って推定することにより、データを表現するための符号長を統計的に短くすることができるという話です。研究のポイントとなる点は、zipなどで使われている性能の良い可逆圧縮アルゴリズムと同等のものがベイジアンノンパラメトリクスに基づいたアルゴリズムで解釈できることを示し、かつ性能も向上させたことです。すごいですね。)
Automatic statistiicianはデータサイエンスにおける究極的な課題の1つなんじゃないかと思います。ただ、質問でもありましたが、決してデータサイエンティストの職業を奪うようなものではなく、あくまで便利なツールであるという位置づけだそうです。
リソースアロケーションの話は実応用で非常に重要です。まぁそれ以前に日本だったらちゃんと複数の確率モデルを作れる人がいないと話にならないですが・・・。
以上です。