作って遊ぶ機械学習。

～基礎的な確率モデルから最新の機械学習技術まで～

グラフィカルモデルを使いこなす！～転移学習を表現してみる～

グラフィカルモデル 動く

さて、今日は以前ご紹介したグラフィカルモデルを使って、転移学習（Transfer Learning）の一例をモデル化してみたいと思います。この記事を読んでいただければグラフィカルモデルを使ったベイズ学習が、機械学習における様々な問題設定に対して柔軟なアプローチを与えてくれることがわかっていただけるかと思います。

 

[必要な知識]

下記をさらっとだけ確認しておくといいです。

 

・グラフィカルモデルによる表現

今日は転移学習の一例をグラフィカルモデルを使って表現し、さらにグラフ上での推論を考えてみたいと思います。最後に、具体的なガウス分布を使った例を用いて簡単な実験をしてみたいと思います。

自分は転移学習に関して取り立てて何かやった経験がないので正直なところあまり深淵な議論はできないのですが、ここではとりあえず

「ある確率変数を推定する課題（ドメイン）が２つあり、それぞれに共通する情報と共通でない情報が存在するような問題設定」

という程度で勘弁してください。そして目標は、２つのそれぞれのドメインを独立に扱うのではなく、片方のドメインのデータを上手に利用して残りのドメインの推定精度を向上させることになります。

 

というわけで、早速ですが次のようなモデルを考えてみました。

f:id:sammy-suyama:20160313033300p:plain

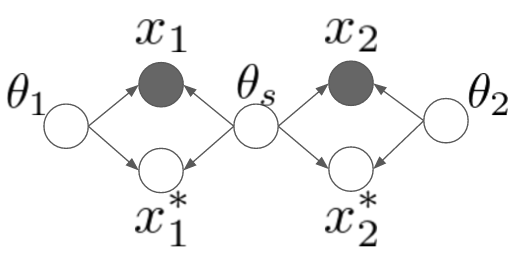
ちょっとややこしいですね。ここでは２つの異なるドメインを取り扱うことにします。一つずつ変数を説明していくと、{x_1}や{x_2}はそれぞれのドメインにおける観測データです。それに対して、星のついている{x_1^*}や{x_2^*}はこれから予測したい未観測データを表します。{\theta_1}と{\theta_2}はそれぞれのドメイン固有のパラメータで、{\theta_s}は両方のドメインでシェアされているようなパラメータです。例えば「平均値はそれぞれのドメインで違うんだけど、分散は共有されている」みたいなモデルを想像してみてください。*1

データが観測されていない状態でのモデルを書き下してみると、

f:id:sammy-suyama:20160313033145p:plain

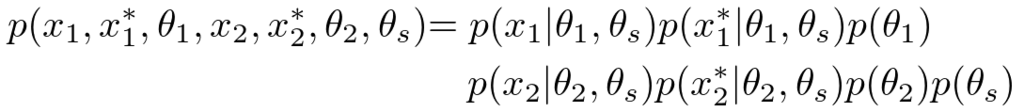
のようになります。ちょっと長くて申し訳ないですが、上のグラフィカルモデルとしっかり対応が取れているか（黒丸を白丸にして）確認してみてください。

 

・推論

さて、次に観測されていない変数たちの事後分布を計算してみることにしましょう。

f:id:sammy-suyama:20160313034830p:plain

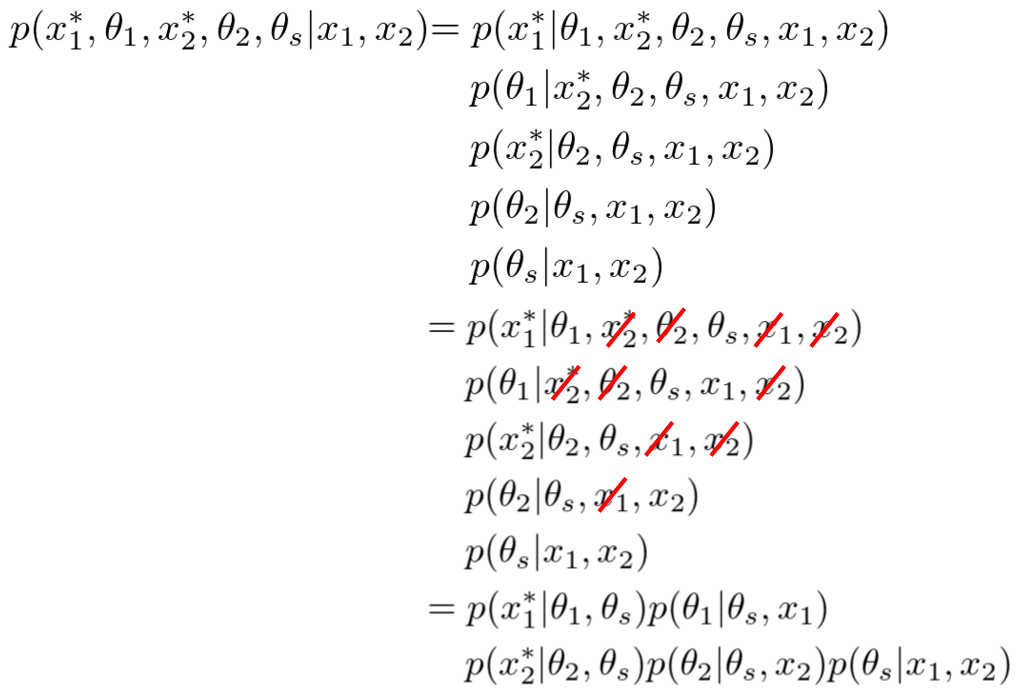
長いですね。一個ずつちゃんと確認すれば難しくはありません。一番最初の右辺は、ただ単に確率のproduct ruleに従って確率変数たちをバラバラに分解してあげただけです。次の式からは、このモデルに対して以前にご紹介した有向分離を適用して変数の独立性を一つ一つ確認し、独立な変数を赤い斜線で消していったものになります。

さて、最後の式を一つ一つじっくり見ていってみましょう。まず一番後ろの{p(\theta_s|x_1,x_2)}ですが、これはドメイン間共有のパラメータである{\theta_s}の分布が両ドメインのデータ{x_1,x_2}から学習できることがわかりますね。次にドメイン{k}に対するパラメータの分布{p(\theta_k|\theta_s, x_k)}は、どちらのドメインでも共有パラメータ{\theta_s}が必要ですが、相手ドメインのデータに関しては興味がないと言っています。最終的な未知変数{x^*_k}の予測は共有パラメータとドメイン固有のパラメータに依存して決まるようですね。

というわけで、上のモデルでは共有パラメータ{\theta_s}が両ドメイン間を仲介することにより、それぞれのドメインで予測したい{x^*_k}の分布がお互いの学習データに依存しあうことがわかりました。

ちなみに、多くの場合では我々はパラメータの確率分布には関心がありません。最終的に求めたいのは、未観測データである{x_1^*}やの予測分布です。この予測分布を式で表現すると次のようになります。

f:id:sammy-suyama:20160314053208p:plain

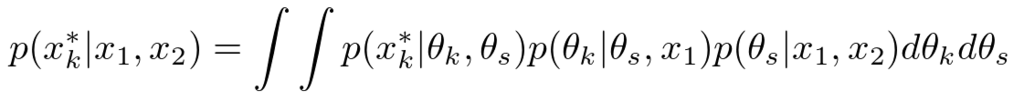
確率のsum ruleを用いて、関心のないパラメータの分布を積分除去（integrate outまたはmarginalize out）してあげただけですね。このようにして求めた分布は周辺分布（marginal distribution）とかって呼ばれたりしています。次の実験ではこの積分操作が解析的に実行できるような確率分布を選んで使うことにします。

 

・実験

さて、上の結果に対して具体的な確率モデルを当てはめて実験してみましょう。今回は画像で見やすいように２次元のガウス分布のモデルを考えます。ドメインが２つあり、それぞれで平均値は違うんだけど、分散パラメータは共通の分布からサンプルされている、というような設定です。ドメイン１における学習データを増やすことにより、ドメイン２の学習結果（分散の値）も変化していく様子を表現してみたいと思っています。できれば具体的な式展開を示してご説明したいのですが、ものすごく長くなってしまうので今回は割愛します。*2

さて、早速ですが実験結果のアニメーションです。

f:id:sammy-suyama:20160314054240g:plain

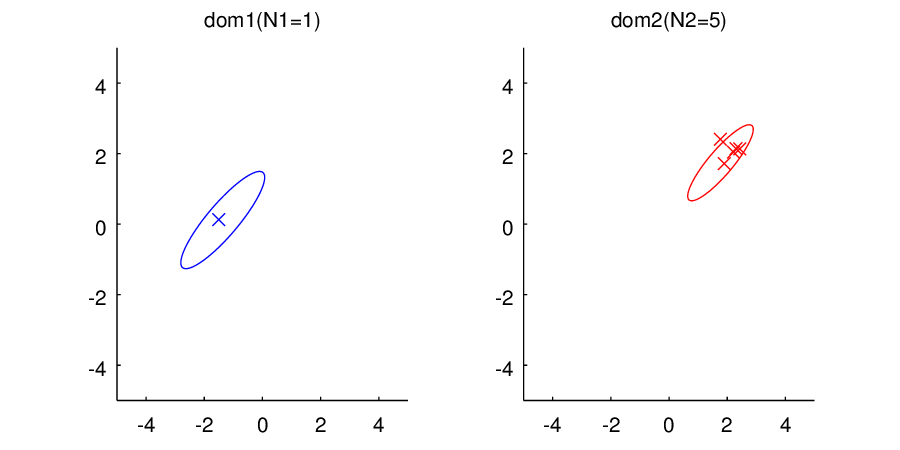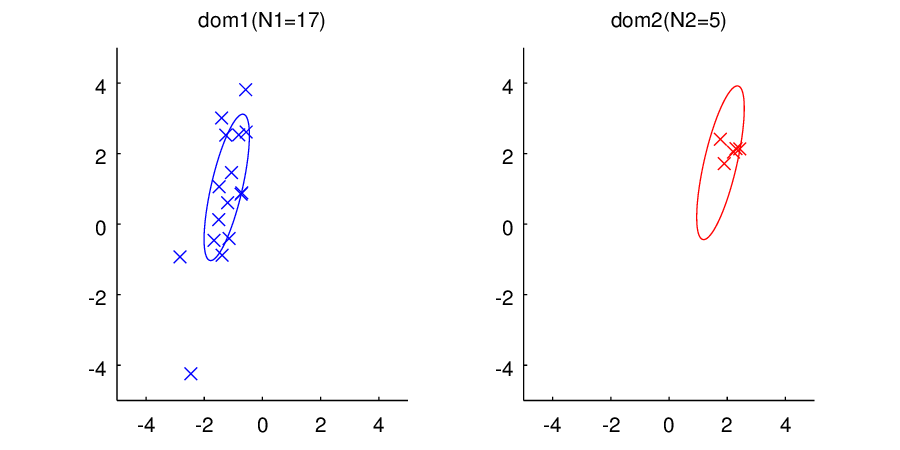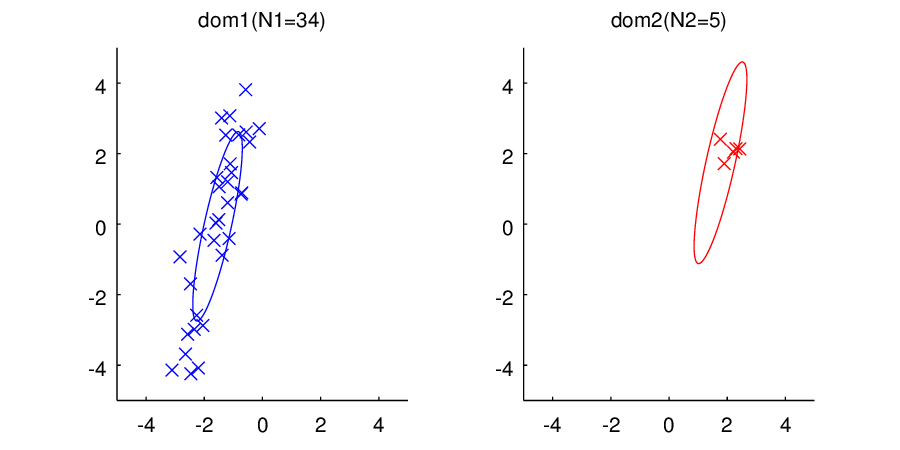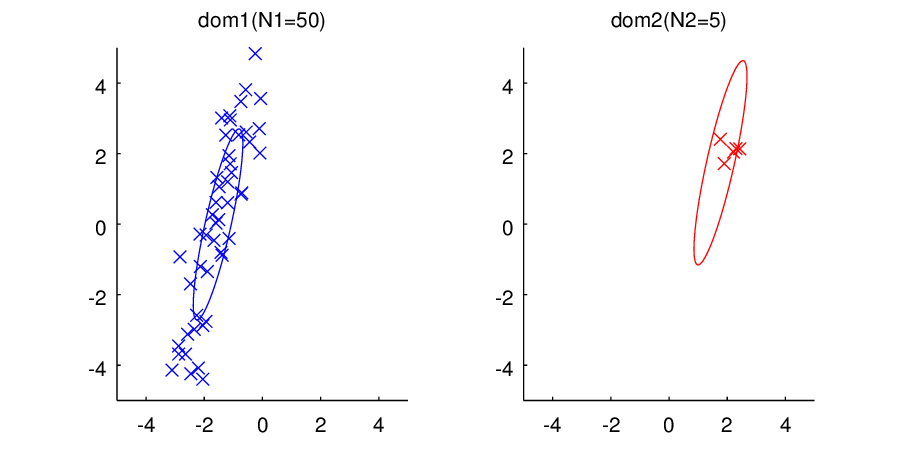
ご覧いただけるように、左側のドメイン1ではデータ数{N_1=1}から順に{N_1=50}まで与えていってあげています。右側のドメイン2はデータ数{N_2=5}で固定したままです。データは左側にしか与えていないにもかかわらず、右のドメインでは分散の形状（楕円）が同じように学習されていっていることに注目してください。

ちなみに、非常に見づらくて申し訳ないのですが、分散の大きさは左右で同じではないです（{N_1=1}のときにかろうじてわかります。）。これは、もともとの分散行列に対する事前分布は同じ設定なのですが、事後分布はデータの与え方によって当然異なってくるためです。データ数が少ないときは左側の分散の方が大きく、データ数が多くなってくると左側の分散の方が小さくなっていきます。

また右側のドメインでは平均値は変化しません。なぜなら、左側で与えられているデータたちは右側のドメインの平均値に対する情報を与えないからです（まぁ、そういう風にモデル化してるからなんですが）。

 

・まとめ

というわけで、今回は転移学習の一例をグラフィカルモデルで表現してみました。今回のようなモデル以外にも例えば「ドメイン1とドメイン２でパラメータは同じだが、データがある関数によって{x_2=f(x_1)}のように変換されている」みたいなモデルを考えることもできます。この場合では、データを生成するパラメータたちと、変換関数のパラメータをデータから学習することになります。モノクロ画像のデータをRGB画像のデータと組み合わせるとか、アングルの異なるセンサーから得たデータを対応付けるとかに使えそうですね。

いずれにしても重要な結論としては、確率モデルを使ったベイズ学習ではいちいち「転移学習」といった固有の課題に対する問題意識は持ちません。実際のデータ解析の現場において、異なるデータ間で何かしら共通する情報があるというのであれば、ただ単に「それをモデル化すればいい」というだけの話になります。

データやデータの裏にある背景を入念に調べ上げ、丁寧にモデル化して推論をする―というのがベイズ推論を使った機械学習の本質です。

*1:うーむ、どんな状況でしょう。例えば世界の都市の人口密度なんかは、平均値（緯度と経度）こそバラバラに散らばっていますが、分散（人口の広がり具合）には共通の傾向があるかもしれないですね。もちろんそこまで単純ではないですが。

*2:今回の実験では、データ観測モデルに対してガウス分布を、平均値と分散のパラメータに対してガウス・ウィシャート分布を使用しています。また、最終的にプロットしている予測分布は多次元のt分布になります。

アニメでわかるベイズ推論によるパラメータ学習

動く

さて、今日はガウス分布を使った簡単な実験を行って、ベイズ推論における機械学習の本質の一端を説明したいと思います。せっかくなので前回取り扱った多峰性事前分布も実験に取り入れてみたいと思います。

 

改めてベイズ学習を数式で書くと次のようになります。

{p(\theta | x) \propto p(x|\theta)p(\theta) }

パラメータに関する事前の知識{p(\theta)}が、尤度関数{p(x|\theta)}を通して、事後の知識{p(\theta|x)}に変換されるんでしたね。今回はこのプロセスをアニメーションを見ながら確認してみようというお話です。

 

で、今回は次のような平均値パラメータ{\mu=0}を持った真のガウス分布のパラメータを推論する問題を考えてみたいと思います。

{N(x|0, \Sigma)}

分散{\Sigma}は簡単化のため、既知で固定ということにしておきます。先ほどのベイズ学習の表記を使うと{\theta = \{\mu \}}ということになりますね。

 

さて、データ{x}に対する観測モデル{p(x|\mu)}はガウス分布を使うとして、事前分布{p(\mu)}は違ったものを３種類用意してみたいと思います。そして実際に真のガウス分布からサンプルされたデータを与えてあげることによって、それぞれの事前分布たちがどのような事後分布に成長していくのかを観察してみたいと思います。

 

＜共役事前分布A＞なだらかな分布を持つ、あまり事前情報のない分布

f:id:sammy-suyama:20160302054954p:plain

 

＜共役事前分布B＞ちょっと偏った思想を持つガンコな分布 

f:id:sammy-suyama:20160302055037g:plain

 

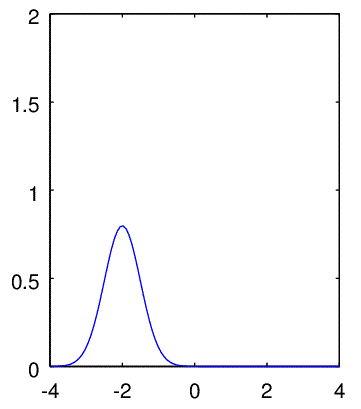
＜多峰事前分布C＞多峰性を持つちょっと優柔不断な分布

f:id:sammy-suyama:20160302055050g:plain

 

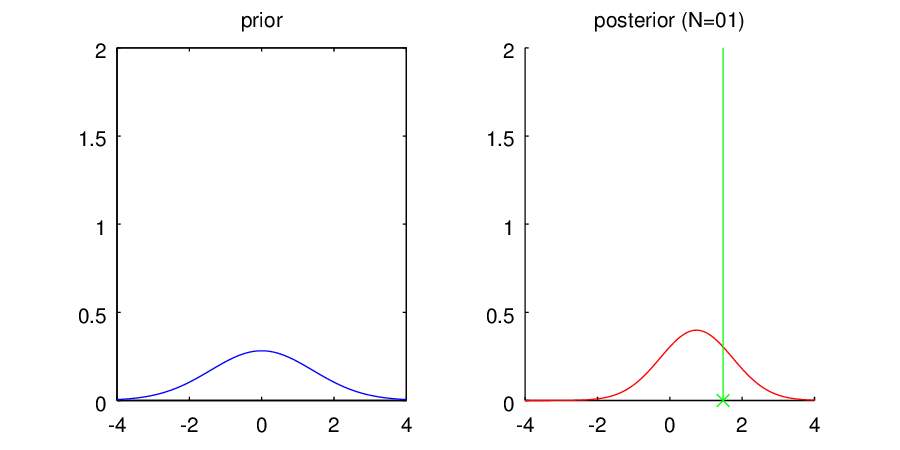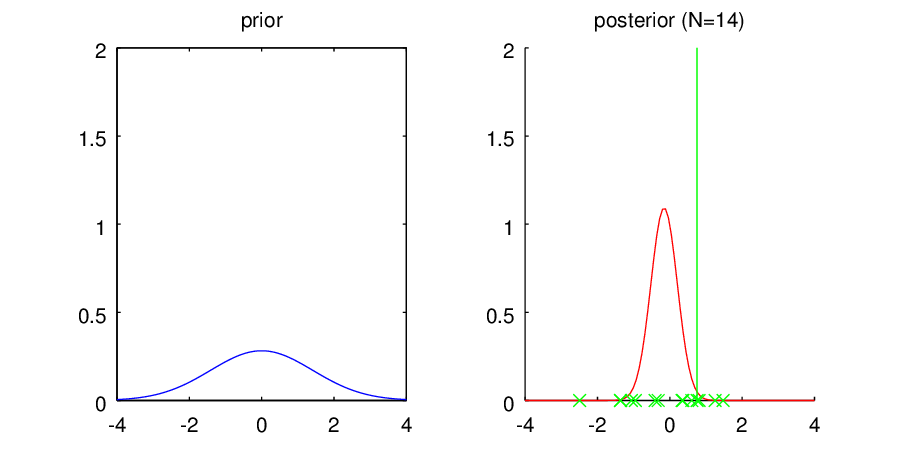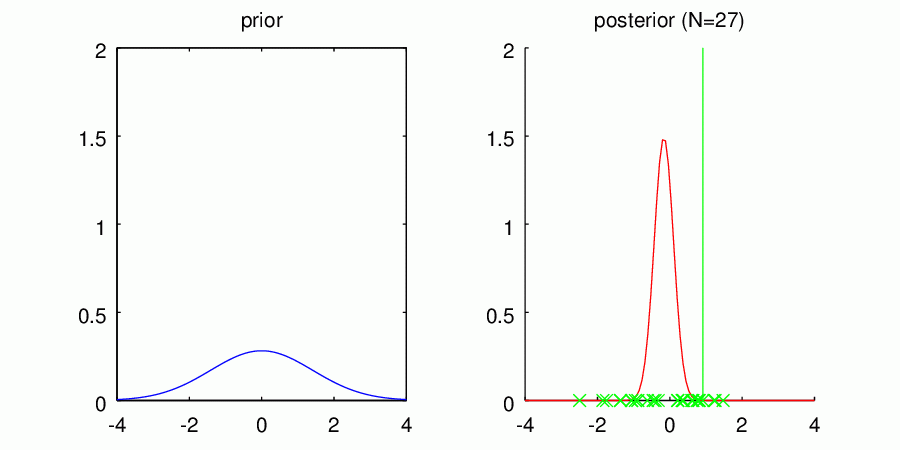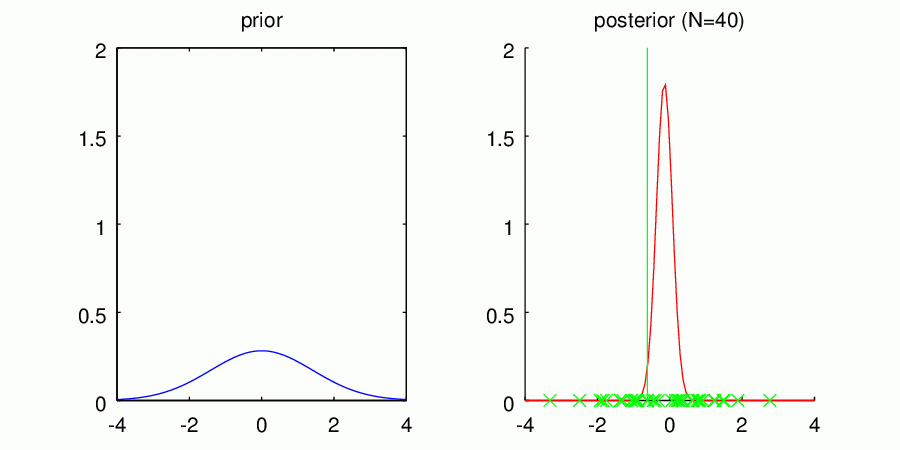
さて、これらの個性的な登場人物に対して、真の平均値0を持つ未知のガウス分布からサンプルされたデータ点を１つずつ与えてあげるとどうなるのでしょうか？アニメを作ったのでご覧ください。

 

・共役事前分布A

f:id:sammy-suyama:20160302055301g:plain

・共役事前分布B

f:id:sammy-suyama:20160302055709g:plain

・多峰性事前分布C

 

f:id:sammy-suyama:20160302055809g:plain

 

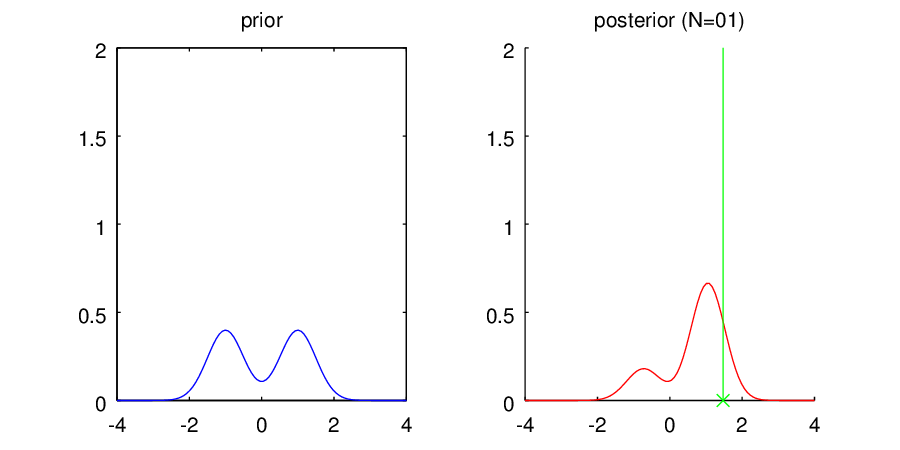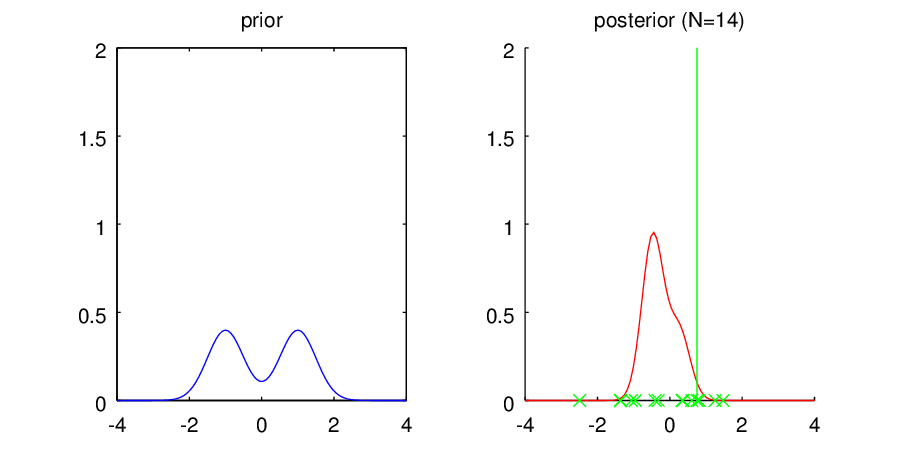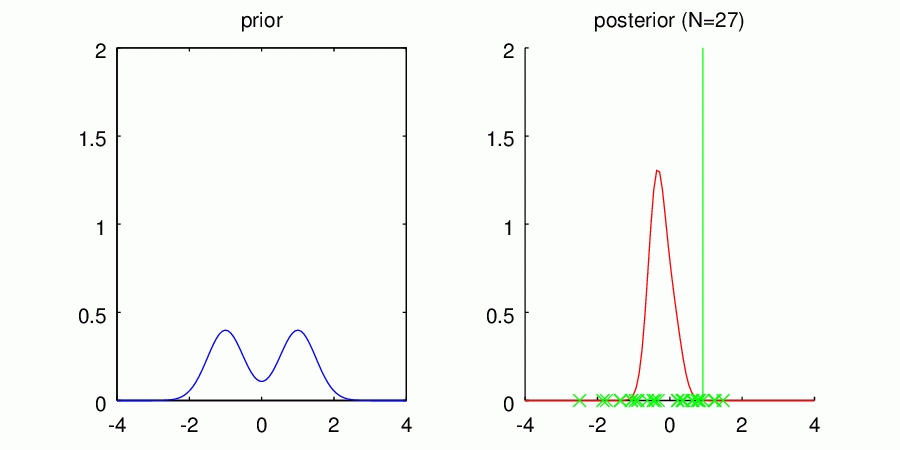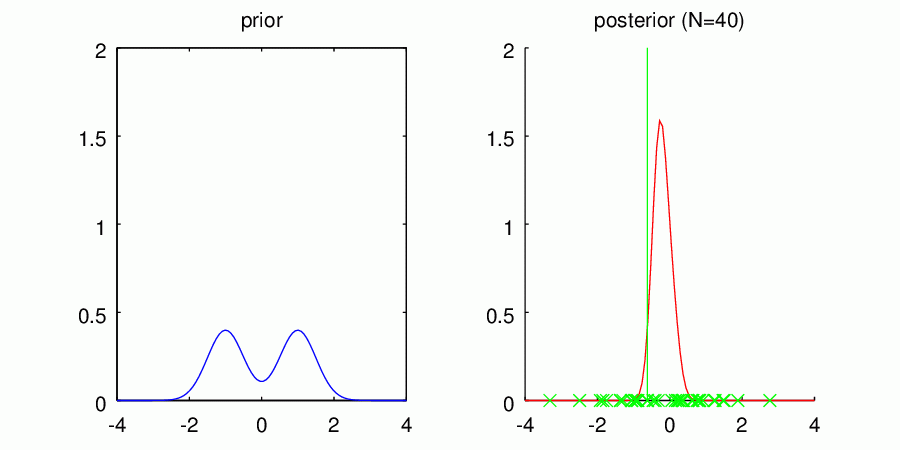
左の図には再びそれぞれの事前分布の形状を表示しています。右の図は観測されたデータを元に計算されたパラメータの事後分布で、ピコピコ現れる縦線は観測されたデータを表しています。得られた分布はデータ点に対する密度分布{p(x)}ではなく、平均値パラメータに関する不確かさ{p(\theta|x)}を表しているので注意してください。細くて0に集中している分布ほど、平均値パラメータが0であることの確信の高さを表しているんですね。

 

さて、改めてデータ数がある程度十分に観測されたとき（４０点）の事後分布を比べてみましょう。

f:id:sammy-suyama:20160305024310p:plain

興味深いのは、それぞれが違う事前分布から学習をスタートしたにもかかわらず、ある程度学習データが集まるとみんな同じような事後分布に収束していることです。ただ、ガンコ者の事前分布Bは未だに最初の知識をほんの少し引きずっているように見えます（平均値が左にずれてますね）。優柔不断だった事前分布Cは、多峰性の形状がほとんど失われ一つのガウス分布に収まっているように見えますが、それでも事前分布Aと比べると若干あいまいさを残した広めの結果になっていますね。

この結果はベイズ学習において、もっとも重要な特性を示しています。データが少ないうちはそれぞれの推論結果は事前分布の形状に大きく左右されます。しかし証拠となるデータがたくさん集まるにつれて、最初の知識による影響は次第に薄れ、すべての事前分布たちが似たような形状の事後分布に収束していきます。

ベイズ推論が「異なった意見を持つ人たちでも証拠さえ十分に集まれば最終的に合意を得る」という、非常に理にかなった原理に基づいていることが分かります。*1

 

さて、この結果から機械学習におけるベイズ学習の利点をいくつか見ることができます。

第１に、ベイズ学習ではデータの数が少ない（最悪の場合0個！）の場合でも何かしらの予測結果をひねり出すことができます。データが少ないなら少ないなりに、事前知識を駆使して何かしらの結果を出してくれるのがベイズ学習の強みです。

第２に、ベイズ学習は複雑なモデルに対する学習においても力を発揮することができます。実際の機械学習の問題では、上記のような単純なガウス分布の平均値を推定するだけの簡単な問題はありません。混合ガウス分布や隠れマルコフモデルに代表されるような、グラフィカルモデルを駆使したはるかに複雑なモデルを使って問題を解くのが通常です。このようなモデルでは学習に必要なデータ数が多くなるのが通常で、「ビッグデータ」といえどもまるで学習データが足りない、というような状況はよく起こります。*2

第3に、ベイズの定理を使ったこのような事前分布から事後分布への学習プロセスは、非常に自然で効率的な逐次学習の手段になります。これは、例えばリアルタイムで学習・予測するようなオンラインシステムを開発する場合や、他のモデルで学習した結果を別のモデルに組み合わせたりする場合に非常に便利な特性です。

 

以上、今回は簡単な実験でベイズ学習の本質に迫ってみました。細かい技術面に注目するとベイズ学習の利点は実はこれだけではありません。また別の機会でベイズ学習におけるモデル選択や予測分布に関するお話をしたいと思います。

*1:ちなみに事前分布で確率0を割り当ててしまった領域に対しては、いくら学習しても合意に至りません。今回のようなガウス分布の例では実数すべての値に対して0ではない確率を割り当てているのでそういったことは起こりませんが、実際のモデルでは、事前のモデルで表現しえないような予測結果は決して得ることができないという事実は、当たり前ですが知っておいた方がいいでしょう。

*2:ビッグデータの本質は、ただ単にデータのレコード数が増えるということではなく、データの次元数が増加することにあると個人的には考えています。予測精度を高めるためには様々なリソースから得られたデータを統合して学習に使う必要がありますが、このような多次元データに対しては、最尤推定や最適化などの手法は簡単にオーバーフィットしてしまうため、ベイズ学習が有効な解決手段になります。

第一線のAI研究者が注目する最新機械学習技術6選（NIPS2015招待講演より）

まとめ

ちょっと前になりますが、昨年12月に行われた機械学習のトップカンファレンスであるNIPS2015の講演ビデオが上がっているようなのでチェックしてみました。今回ご紹介するのはケンブリッジ大学のZoubin Ghahramani教授の研究です。

datasciencereport.com

同教授は今後excitingな機械学習の基礎・応用に関する取り組みとして次のような６テーマを紹介しています。

 

・Bayesian Nonparametrics

ベイジアンノンパラメトリクスでは、無限次元を持つモデルを仮定することにより、データ量に応じて適切なモデルを学習することができます。こういったモデルは関数上の確率分布（確率過程）を考慮することによって実現できます。代表的な例はガウス過程、中華料理店過程、インド料理過程などです（ご飯ばっかりですね）。

ガウス過程は、回帰や識別、ランキングや次元削減に使われています。またある種のニューラルネットワークがガウス過程の一例であることが1994年に示されているそうです。

・Probabilistic Programming

確率モデルを構築し、推論アルゴリズムを導き、実装をする・・・といったプロセスはものすごく時間がかかって大変です。Probabilistic programmingは確率モデル（あるいは確率的にデータを生成するプロセス）を記述するための言語で、推論はサンプリングや変分近似で勝手にやってくれます。代表的なのはBugsやStanです。

・Bayesian Optimization

日本語だと「ベイズ的最適化」の名前でコンセンサスが取れていたと思います。ガウス過程を使い未知の関数の最適値を探す手法です。未知の関数の評価にとても時間orコストがかかるような状況を仮定しており、いかに少ない評価回数で最適値を探せるかがポイントになります。

・Data Compression

シャノンの定理によると、すべての圧縮アルゴリズムは確率モデルに基づくそうです。ベイジアンノンパラメトリクスを使ったアダプティブな圧縮アルゴリズムが近年非常によい圧縮性能を出しているようです。

・Automatic Statistician

データを食わせるだけで何かしらレポートを返してくれるような野心的なアルゴリズムの話です。アイデアは非常にシンプルで、いくつかのカーネルを組み合わせて周辺尤度を評価することによって、データをうまく説明するような適切なモデルを探索します。

・Rational Allocation of Computational Resources

大量のデータと複数のモデルがある中、リソース（時間、CPU、メモリ、ディスクサイズ）が限られた状況下でいかに最適な機械学習システムを構築するか、という課題設定です。これを不確実性がある中での逐次的な意思決定問題として扱います。

 

・個人的な雑感

Bayesian nonparametricsは従来のベイズ学習に対する正当な拡張であるため、今後も基礎的な研究は発展していくかと思います。そろそろ大きなアプリケーションがほしいところですが、ディープラーニングなどの成功しているモデルもかなりの部分はこれに置き換わり、より洗練されたアルゴリズムになるのではないかと予測しています。

Probabilistic programmingは基本的に推論性能はあまりよくないようです。僕は使ったことがないのですが、とりあえず複数のモデルを素早く試したいときなんかには便利だと思います。普通にモデル構築→アルゴリズム導出→実装ってやってるとそれだけで１日使いますからね・・・。

ベイズ的最適化は非常に概念もわかりやすく応用先も広いのでぜひ多くの人に使っていただきたいと思います。日本の京などのでっかいコンピュータで何かシミュレーションを行う場合は、Bayesian optimizationで全体を包んであげると解探索が早くなるかもしれません。あまりいないと思いますが、例えば遺伝的アルゴリズムとかを使っている人は早々にこちらへの置き換えを検討した方が良いと思います。

データ圧縮も面白い領域です。結局のところ、jpegに代表されるように、非可逆圧縮というのはデータの中の捨ててもいい情報と残さなきゃいけない情報をうまく見つけることが基本になっています。これは機械学習における特徴量抽出といっしょです。画像だったら、人間が認知に必要でない情報は捨ててもいい可能性が高いと言えるわけですね。データ圧縮もかなりドメイン依存が強いかと思いますが、汎用的なアルゴリズムでどこまでいけるのかは興味深いですね。 （追記：すみません、招待講演の内容では「非可逆圧縮」ではなく、情報損失のない「可逆圧縮」の話だったようです。データに関する分布をベイジアンノンパラメトリクスを使って推定することにより、データを表現するための符号長を統計的に短くすることができるという話です。研究のポイントとなる点は、zipなどで使われている性能の良い可逆圧縮アルゴリズムと同等のものがベイジアンノンパラメトリクスに基づいたアルゴリズムで解釈できることを示し、かつ性能も向上させたことです。すごいですね。）

Automatic statistiicianはデータサイエンスにおける究極的な課題の１つなんじゃないかと思います。ただ、質問でもありましたが、決してデータサイエンティストの職業を奪うようなものではなく、あくまで便利なツールであるという位置づけだそうです。

リソースアロケーションの話は実応用で非常に重要です。まぁそれ以前に日本だったらちゃんと複数の確率モデルを作れる人がいないと話にならないですが・・・。

 

以上です。

多峰性の事前分布ってどうやって作るの？

グラフィカルモデル

ベイズ学習では、複雑なモデルにおけるパラメータの学習を効率的に行うために、しばしば観測モデルに対する共役な事前分布を仮定します。例えばベルヌーイ分布のパラメータの事後分布を推定するために、事前分布をベータ分布にしたりします。ウェブを検索すると様々な確率分布のパラメータに対応する共役事前分布のリストを見つけることができますが、そもそも、データを表現する観測モデルが決まってしまうと自動的にそのパラメータの事前分布が決まってしまうのは何だか窮屈な感じがしてしまいます。

今回はグラフィカルモデルを工夫することによって、もっと自由な、例えば多峰性の事前分布などを簡単に作れることをお話ししたいと思います。

 

[必要な知識]

下記をさらっとだけ確認しておくといいです。

 

さて、改めてベイズ学習におけるパラメータの学習を書いてみると次のようになります。

{ p(\theta| x) \propto p(x|\theta)p(\theta) }

ここで{x}は観測データ、{\theta}はモデルのパラメータです。さらに{p(\theta|x)}はパラメータの事後分布、{p(x|\theta)}は尤度関数、{p(\theta)}はパラメータの事前分布と呼ばれています。ベイズ学習を言葉に翻訳すると、

「パラメータに関する我々の事前知識{p(\theta)}は、観測データに対するモデルの尤もらしさ{p(x|\theta)}を通して、事後の知識{p(\theta|x)}に変換される」

というプロセスになります。

で、今回は尤度関数を計算するモデルとして次のようにガウス分布を仮定します。

{ p(x| \theta) = \mathcal{N}(x| \mu, \Sigma_x ) }

ここで今回推定したいパラメータは平均値{\theta=\mu}であり、分散{\Sigma_x}に関しては既知で固定であるものとします。

 

・単峰性事前分布によるガウス分布の推定

まず始めに、ガウス分布の平均値パラメータに対する一番シンプルな事前分布の選び方は、共役事前分布であるガウス分布を使うことです。*1

{ p(\mu) = \mathcal{N}(\mu | m, \Sigma_{\mu}) }

ここで{m}と{\Sigma_{\mu}}はそれぞれ平均値と分散パラメータであり、{\Sigma_x}と同様固定値であるものとします。

このモデルに対して{N}個のデータを観測した後の事後分布は、グラフィカルモデルで表現すると次のようになります。

f:id:sammy-suyama:20160220183059p:plain

さて、さっそく事後分布を計算してみましょう。事後分布はベイズの定理から次のように計算できます。

{ p(\mu|x) \propto p(x|\mu)p(\mu) }

両辺対数を取って計算を進めることにします。{\mu}に関する分布を求めたいので、無関係な項はすべて定数項{c}に吸収させてしまいます。

f:id:sammy-suyama:20160220215841p:plain

結果はやはりガウス分布になり、新たに文字{\hat{m}}と{\hat{\Sigma}_{\mu}}を導入すれば次のように書けます。

f:id:sammy-suyama:20160220220026p:plain

・多峰性事前分布によるガウス分布の推定

さて、今度は先ほどの単純な共役事前分布と違い、{\mu}に対して{K}個の異なる平均値の分布からなる、多峰性の事前分布を構築してみましょう。感覚的な例をいうと、推理小説で「犯人が一人なのはわかっているけど、容疑者が複数いる」というような状況設定です。

これは次のグラフィカルモデルで示すように、新たな潜在変数{z}を導入することによって実現できます。

f:id:sammy-suyama:20160220183117p:plain

まず始めに新しく登場した{z}に対する確率分布を定義してみましょう。ここではもっとも単純な離散変数の分布であるカテゴリカル分布を使います。

{\begin{eqnarray} p(z) = Cat (z|\pi) = \prod_{k=1}^{K} \{ \pi^{(k)} \}^{z^{(k)}} \end{eqnarray} }

ただし{\sum_{k=1}^{K} \pi^{(k)}=1 }です。さらに、{\mu}の分布は次のように{z}の条件付き分布になります。

{ \begin{eqnarray} p(\mu|z) = \prod_{k=1}^{K} {\mathcal{N}(\mu| m^{(k)}, \Sigma_{\mu}^{(k)})} ^{z^{(k)}} \end{eqnarray} }

このような{z}に対する記法は1 of K表記というように呼ばれたりします。例えば{z=(0,0,1,0)}のように、{z}の{K}個ある要素のうち一つだけが１を取ることによって、どの分布が使われるのかを指示（indicate）することができます。

それでは事後分布を計算してみることにしましょう。

{p(\mu, z| x) \propto p(x,\mu,z) = p(x|\mu)p(\mu|z)p(z) }

今回は{\mu}と{z}の2つの事後分布を求めなければなりませんが、これはそれぞれ別々に解析的に計算できます。まず上の数式から{\mu}に関わる項のみを取り出してみましょう。例によって対数計算を行うと、

{ \ln p(x,\mu,z) = \ln p(x|\mu) + \ln p(\mu|z) + c }

となります。先ほどの単峰性の例と同じように{\mu}のみに注目して計算を行うと、結果として{\mu}の事後分布は{z}に依存する形となり、次のような（条件付き）ガウス分布になります。

f:id:sammy-suyama:20160220220259p:plain

さて、今度は{z}の事後分布も求めてみましょう。これは{\ln p(z|x) = \ln p(\mu|z) - \ln p(\mu|z,x)}を考慮すれば簡単に計算できます。

{ \begin{eqnarray} \ln p(z|x) = \sum_{k=1}^{K} z^{(k)} (-\frac{1}{2} {\mu^{(k)}}' \Sigma_x^{-1} \mu^{(k)} -\frac{1}{2} \ln |\Sigma_{\mu}^{(k)}| \\ +\frac{1}{2} {\hat{\mu}^{(k)}}' \hat{\Sigma}_x^{-1} \hat{\mu}^{(k)} +\frac{1}{2} \ln |\hat{\Sigma}_{\mu}^{(k)}| +\ln \pi^{(k)})+c \end{eqnarray} }

{z}に掛け算されている部分が事後分布のパラメータになります。書き直すと次のようになります。

{ \begin{eqnarray} p(z|x) = Cat (z|\hat{\pi}) = \prod_{k=1}^{K} \{ \hat{\pi}^{(k)} \}^{z^{(k)}} \end{eqnarray} }

{\hat{\pi}}は次のように計算されます。

{ \begin{eqnarray} \hat{\pi}^{(k)} \propto exp\{ -\frac{1}{2} {\mu^{(k)}}' \Sigma_x^{-1} \mu^{(k)} -\frac{1}{2} \ln |\Sigma_{\mu}^{(k)}| \\ + \frac{1}{2} {\hat{\mu}^{(k)}}' \hat{\Sigma}_x^{-1} \hat{\mu}^{(k)} +\frac{1}{2} \ln |\hat{\Sigma}_{\mu}^{(k)}| +\ln \pi^{(k)} \} \end{eqnarray} }

実装上は{\hat{\pi}}が足して1になるように正規化してください。

以上、事後分布{p(\mu,z|x)}を見てみると、事前分布{p(\mu,z)}と同じ形状を持っていることになります。ガウス分布の平均値だからといって単純にガウス事前分布を使う必要はなく、今回のような多峰性のガウス分布を事前分布にしても、最適化のような計算をせずに解析的に事前分布と同じ関数形の事後分布が求まるんですね。*2

 

さて、ちょっと思った以上に計算式ばかりの記事になってしまったので今日は一旦ここで切ります。今回はガウス分布の平均値パラメータの事後分布を推定する例を使って、多峰性の事前分布をどのように構築したらよいのかを説明しました。次回は今回紹介した事前分布を使った簡単な実験を行い、ベイズ学習における興味深い特性に関してお話したいと思います。

 

＝＞続きの記事はこちらです。

アニメでわかるベイズ推論によるパラメータ学習 - 作って遊ぶ機械学習。

 

*1:ガウス分布の平均値の共役事前分布は「たまたま」ガウス分布になります。ガウス分布を観測、平均値ともに使っているので気を付けてください。

*2:ちなみにこの多峰性事前分布によるモデルは、混合ガウス分布とは異なります。混合ガウス分布の場合は潜在変数がデータ{x_n}ごとに割り当てられます。今回の例と違い、解析的に求めることは不可能で、変分近似のような近似推論法を使う必要があります。

グラフィカルモデルを使いこなす！～有向分離の導入と教師あり学習～

グラフィカルモデル ベイズで解釈

さて、前回はグラフィカルモデルの描き方と簡単な事後確率の推論をやってみました。今回以降は、下記のようなもう少し現実的な確率モデルに対する推論をグラフィカルモデル上でやってみる予定です。

 

・教師あり学習（今回）

・半教師あり学習

・共変量シフト

・転移学習

・潜在変数モデル（EMアルゴリズム）

 

今回は導入として、有向分離（D-separation）と呼ばれる、より複雑なモデルに対する確率変数の独立性をチェックするための手法を紹介します。これを使って、教師あり学習である回帰モデルや識別モデル（2つともグラフィカルモデル上の区別はないです）に対する推論結果がどうなるかを見てみたいと思います。

  

今回やることも基本的には前回の３つのノードを使った単純なグラフィカルモデルと同じです。

machine-learning.hatenablog.com

あるグラフィカルモデルが与えられ、さらに一部のノードが観測されたとき、残りの観測されていないノードの確率分布（事後分布）を計算します。このとき事後分布は一般的には複数の確率変数が絡みあった複雑な形状をしてしまっています。グラフィカルモデルから変数間の独立性を読み取り、事後分布をよりシンプルな積に分解して表すのが今回の課題になります。

というわけで、その独立性を発見するためのシステマチックな手法である有向分離をさっそく紹介します。

 

＜有向分離（D-separation）＞

与えられたグラフィカルモデル上でノードＡとノードＢが独立であるか判断したいとします。AとB間の間のすべての経路がブロックされていればＡとＢは独立になります。あるノードCが経路をブロックしているかどうかを判定するには次のフローチャートを使います。

f:id:sammy-suyama:20180813144416p:plain

むむ、なんだかでかい図が出てきてちょっと嫌な感じです。慣れないうちは非常にめんどくさそうな手続きに見えてしまいますが、慣れてもめんどくさいので諦めてください。この図は次の具体的なモデルで使っていきましょう。

 

・具体例）教師あり学習

では、今回は教師あり学習をグラフィカルモデルで表現し、それに有向分離を適用してみましょう。一番単純な教師あり学習は回帰・識別モデルです。これはグラフィカルモデルでは次のように書くことができます。

f:id:sammy-suyama:20160213234013p:plain

$x_1$と$y_1$は教師あり学習のための訓練データということにしてください。そして$x_2$と$y_2$はテストデータです。$\theta$は$x$から$y$を推定するための未知のパラメータです。$y$が連続変数を取る場合は回帰で、離散値を取る場合は識別（分類）になります。このグラフに対応する式も書いておきましょう。

\[ p(y_2, x_2, y_1, x_1, \theta) = p(y_2|x_2, \theta)p(x_2)p(y_1|x_1,\theta)p(x_1)p(\theta)\]

グラフと式をよく見比べて対応が取れていることを確認してみてください。モデル作りはこのようにまだデータが1つも観測されていない状態からスタートします*1。

実際には、教師あり学習では、$x_1$と$y_1$が訓練データとして観測され、さらに予測したい$y_2$に対する入力値$x_2$が観測されます。描き直してみましょう。

f:id:sammy-suyama:20160213230120p:plain

手元に持っている観測データが条件付けられましたね。ついでに式も書いておくと次のようになります。

\[ p(y_2, \theta | x_1, y_1, x_2) \]

さて、この分布を単純化してみることにしましょう。まず始めに、確率の乗法定理を使って事後分布を積の形で書いてあげます。

\[p(y_2, \theta | x_1, y_1, x_2) =p(y_2| \theta, x_1, y_1, x_2)p(\theta | x_1, y_1, x_2)\]

単純に$y$と$\theta$を2つの項に分けて書いてみただけです。まだちょっと式が長いので、ここでいよいよ有向分離を導入して2つの項をそれぞれダイエットしてみることにしましょう。

 

・$p(y_2| \theta,  x_1, y_1, x_2)$の項をダイエット

さて、この項をグラフィカルモデルで描いてみましょう。この項では$\theta$が条件付けられているので黒丸になります*2。

f:id:sammy-suyama:20160213230508p:plain

さて、$y_2$と他の変数たちの独立性を見ていきましょう。まず始めに、$y_2$と$\theta$は独立でしょうか？そんなわけないですよね。なぜなら2つのノードは隣り合っているので、どうあがいても依存してしまいます。同様の理由で$x_2$も隣にいるので依存してしまいます。

では、$y_1$はどうでしょうか？$y_2$と$y_1$の間の経路は、$\theta$を経由する以外にはありません。したがって、$\theta$が2つのノードをブロックしているかどうかを確かめればOKです。ということで、先ほどのフローチャートを使ってみましょう。

  1. $\theta$は●？  Yes!
  2. $\theta$は→●←？ No!   =>   ブロックする（B1）

はい、どうでしょうか。ちゃんとB1の結果にたどり着けたでしょうか？$\theta$が$y_2$と$y_1$を結ぶための唯一の経路をブロックしてしまっているので、２つの変数は独立であることが分かります。同じ理由で$y_2$と$x_1$の経路も$\theta$によってブロックされますね。

というわけで、$y_2$に対して、$\theta$と$x_2$には依存関係があり、$y_1$と$x_1$に対しては独立であることがわかりました。これで式が次のようにダイエットできます。

\[ p(y_2| \theta,  x_1, y_1, x_2)=p(y_2| \theta, x_2) \]

 

・$p(\theta | x_1, y_1, x_2)$の項をダイエット

さて、この項も改めてグラフィカルモデルを描いてみましょう。

f:id:sammy-suyama:20160213230527p:plain

この項では$y_2$が登場していないので点線で描いてみました。

さて、ここから$\theta$と他の確率変数との依存性を見ていきます。まず見た瞬間すぐにわかるのは、$x_2$とは独立であるということです。経路そのものが存在しませんよね。

一方で$y_1$は隣り合っているので依存してしまいますね。

では$x_1$はどうでしょうか？先ほどと同様、$\theta$と$x_1$の間の経路を見てみると、唯一、$y_1$が間にいます。これが経路をブロックしているかどうかをフローチャートを使って調べればOKですね。

  1. $y_1$は●？  Yes!
  2. $y_1$は→●←？ Yes!   =>   ブロックしない（UB1）

おっと、さっきと違って経路上のノードがブロックしませんね*3。この場合は、$\theta$と$x_1$は依存することがわかりました。したがってこの項では$x_2$のみが消えて

\[ p(\theta | x_1, y_1, x_2) =p(\theta | x_1, y_1)\]

となることがわかります。

 

さて、ちょっと長かったですが、以上、教師あり学習のモデルに対する事後分布を考えると次のような形になることがわかりました。

\[p(y_2, \theta | x_1, y_1, x_2)=p(y_2| \theta, x_2)p(\theta | x_1, y_1)\]

この式の意味するところを解釈してみましょう。

まず右側の$\theta$の分布を見てください。この分布は、パラメータ$\theta$の分布を学習するには訓練データである$x_1$と$y_1$だけ必要だよ、と言っています。テスト入力$x_2$は学習には影響しないようですね。次に左側の$y_2$の分布を見てみると、未観測である$y_2$の分布を推定するためにはパラメータ$\theta$と入力値$x_2$のみが必要で、過去の学習データである$x_1$は$y_1$がどうだったかなんて知らないよ、と言っています。これは教師あり学習のひとつのシンプルさであり、また制限でもあると言えます*4。

ちなみに、実際の応用の場面では学習後の$\theta$なんかどうでも良くて$y_2$の予測だけが知りたいということが多いと思います。この場合は次のように確率の加法定理を使って$\theta$を消してあげる操作が必要になります。これは周辺化（marginalization）と呼ばれています。

\[p(y_2 | x_1, y_1, x_2)　= \int p(y_2| \theta, x_2) p(\theta | x_1, y_1) d\theta \]

この式が簡単に計算出来るかどうかは具体的な確率分布（ガウス分布など）の設定の仕方に依ります。*5

 

さて、ちょっと長くなってしまったので「めんどくさ」って思われている方もいるかもしれません。しかし、今回の教師あり学習の例をよく振り返って見ると、ベイズ学習で行っていることは確率モデルを設計してその事後確率を推定しただけです。ベイズ推定が最尤推定を発展させたものとして説明されているのをよく教科書とかで見かけますが、そうではなく、単に確率の加法定理と乗法定理を使って条件付き確率分布を求めているだけと捉えると、ベイズの考え方のシンプルさがわかっていただけるかと思います。

 

次回以降はもっと複雑なモデルに対して有向分離を適用し、事後確率を求めていきたいと思います。

*1:グラフ上ではまるで訓練とテストでデータが１つずつしかないように見えますが、今回の例ではデータが$N$個ある場合でも同じ議論になるので省略しました。

*2:黒丸が「観測データ」だと思い込んでいるとちょっと混乱するかもしれません。この項は$\theta$がある値で条件付けられた場合の$y_2$の確率分布を表しています。

*3:ブロックしないということは，「２つのノードの間の独立性をグラフからでは示せない」ということを意味しています．グラフ上では独立でないように見えても，具体的な数式によるモデル化次第では独立にもなり得ることに注意してください．一方，経路がすべてブロックされる場合は独立性は成り立ちます．

*4:発展的話題ですが、テストデータの入力$x_2$もパラメータの学習に含めたい場合は、共変量シフトと呼ばれる入力$x$の分布を考慮する学習モデル等を考える必要があります。また学習データそのものによって柔軟に未知変数の分布を推定したい場合には、ガウス過程等のカーネルモデルを使う必要があります。

*5:この例だと、例えば$p(y|x)$に対してガウス分布を設定し、$p(\theta)$に対して共役事前分布であるガウス・ウィシャート分布などを設定すれば解析的に計算できます。また別の機会で具体的な計算方法を説明したいと思います。

グラフィカルモデルによる確率モデル設計の基本

グラフィカルモデル

今回から数回にわたって、グラフィカルモデルを利用した確率モデルの設計についてお話しします。従来の統計モデルと比べ、機械学習を機械学習たらしめているものの一つは、扱う現象の複雑さにあると言えます。複雑な現象を解析するためにはそれに見合った複雑なモデルが必要で、それを簡潔に記述するための方法としてグラフィカルモデルが開発されました。

「グラフィカルモデルを使って現象をモデル化し、必要に応じて近似推論法を用いて未知の値を推定する」

という一連の流れが身につくと、いろんなデータサイエンスの課題に対してシンプルかつフォーマルに取り組めるようになります。

 

それではまず始めに、超超超重要な確率の加法定理と乗法定理の確認をしてみましょう。 

・加法定理（sum rule）*1 

\[ p(x) = \sum_y p(x,y) \]

・乗法定理（product rule）

\[ p(x,y) = p(x|y)p(y) \]

 

$p(x,y)$は同時分布（joint distribution）と呼ばれ、対称性$p(x,y) = p(y,x)$が成り立ちます。$p(x|y)$は条件付き分布（conditional distribution）と呼ばれ、$y$が与えられた時の$x$の分布です（$y$の分布ではありません）。

ベイズ学習と呼ばれる機械学習の技術は、実は上の2つのルールをただ黙々と使っているに過ぎません。残りは、これらを具体的に計算するための部品である確率分布たちと、（必要に応じて使う）近似推論くらいしかありません。

また2つのルールから有名なベイズの定理が導けますので、重要な結果として覚えておいて損はないです。

・ベイズの定理（Bayes' theorem） 

\[ p(x|y) = \frac{p(y|x)p(x)}{\sum_x p(x,y)} \]

 

さらに用語として知っておいてほしいのが独立です。次の式が成り立つときに限り、$p(x)$と$p(y)$は独立であると言います。

\[ p(x,y) = p(x)p(y)\]

ちなみに両辺を$p(y)$で割ってあげると、分布の独立性は次のようにも書けます。

\[ p(x|y) = p(x)\]

これも覚えておいて損はないです。

 

さて、ここからが今日の本題なのですが、今回はDAG（Directed Acyclic Graph）と呼ばれる、ループ構造のないもっともポピュラーなグラフィカルモデルを扱うことにします*2。まず上記の表記を使った確率モデルと、ノードと矢印を使ったDAGとがどのように対応付けられるのかを確認したいと思います。こういうのは細かい定義をうだうだ言う前に例示した方が早いかと思います。 

 

モデル１） head to tail

f:id:sammy-suyama:20160209232422p:plain

3つの白丸ノードA,B,Cが右向きの矢印のみでつながっています*3。白丸が3つなので確率モデルの式も次のように3つの分布の積で書けます。

\[ p(A,B,C)=p(A)p(B|A)p(C|B) \tag{1} \]

ノードそれぞれに対して確率分布を$p(\cdot)$を置き、矢印の元になっているノードを「条件」として右側に書けばいいんですね。

さて、もしこのモデルでノードBが「観測」された場合はどうなるのでしょうか。「観測」とは、確率変数に具体的な数値が与えられるという意味です（条件付けられる、の方がより正確です）。グラフィカルモデルでは観測されたノードは黒丸で表現されます。

f:id:sammy-suyama:20160209233138p:plain

はい、こんな感じです。このとき、AやCの確率分布はどうなるのでしょうか。Bは黒丸なのでもはや分布を持たず、白丸だけの分布を考えればOKですね。

\[p(A,C|B)\]

ということで、これを式(1)と、確率の加法定理と乗法定理を使ってちょこっと計算してみましょう。

\[p(A,C|B) = \frac{p(A,B,C)}{p(B)} = \frac{p(A)p(B|A)p(C|B)}{p(B)} = p(A|B)(C|B) \]

というわけで、ノードAとCは、Bが観測された状態では「独立になる」ことがわかりました。これは条件付き独立って呼ばれています。あるいは「BはAとCをブロックする」という言い方もします。

モデル１におけるこの結果はとても重要です。一度Bが観測されてしまえばAとCの値は相関を持たなくなるんですね。

 

モデル2） tail to tail

 

f:id:sammy-suyama:20160209233550p:plain

さて、AB間の矢印の向きが先ほどと違い、今度はノードBがA,Cの親になっているような状態です。式で書くとこんな感じです。

\[ p(A,B,C) = p(B)p(A|B)p(C|B) \tag{2} \]

先ほどと同様、Bを観測してみることにしましょう。

f:id:sammy-suyama:20160209233607p:plain

この事後分布が先ほどの例のように条件付き独立になるかどうか計算してみましょう。

\[ p(A,C|B) = \frac{p(A,B,C)}{p(B)} = \frac{p(B)p(A|B)p(C|B)}{p(B)} =p(A|B)p(C|B) \]

はい、というわけで今度もまたAとCはBが与えられたとき独立になるようです。ノードBはAとCをブロックする、と言うんでしたね。

 

モデル3） head to head

f:id:sammy-suyama:20160209234931p:plain

最後ですが、このhead to headと呼ばれる3つ目のモデルが一番のやっかいものです。これを説明したいがために前の2つのモデルを紹介したと言っても過言ではありません。

対応する式は次のように書けます。

\[ p(A,B,C) = p(A)p(C)p(B|A,C) \tag{3} \]

今までのモデルと違い、2つの変数が条件付けられているような項$p(B|A,C)$が出てきましたね。ちなみにこのとき、グラフから読み取っても直感的かと思いますが、AとCは独立です。念のため加法定理を使って調べてみましょう。

\[ p(A,C) = \sum_B p(A,B,C) =\sum_B p(A)p(C)p(B|A,C) = p(A)p(C) \]

$\sum_B p(B|A,C)=1$を使ったのは大丈夫でしょうか。Bの確率分布なので足し合わせれば絶対に1ですね。というわけで、AとCは独立です。これは観測されていないノードBがAとCをブロックしている、とも言えます。

さて、次にBを条件付けしてみましょう。

f:id:sammy-suyama:20160209234943p:plain

今までどおり、対応する事後分布が条件付き独立になるか調べてみましょう。

\[ p(A,C|B) = \frac{p(A,B,C)}{p(B)} = \frac{p(A)p(C)p(B|A,C)}{p(B)} \]

これは他の2例と違って一般的に$p(A|B)p(C|B)$に分解することは出来ません。これ以上どんなに式をコネくり回してもダメです。もともとは独立だったAとCが、Bが観測されることによって互いに依存するようになってしまいました。

このように、モデル3ではBを観測することによって、AとCの分布がより複雑なものになってしまいました。実はこの現象が、ベイズ学習において近似推論手法（変分近似*4やMCMC*5）が必要とされる理由なんですね。

 

さて、今回はグラフィカルモデルの導入と、簡単なモデルにおける事後分布の推論を見てみました。次回は有向分離と呼ばれる、もっともっと複雑なグラフィカルモデルに対するノードの独立性の判定アルゴリズムを紹介します。さらに、具体的ないくつかの例（教師なし学習、回帰・識別、半教師あり学習、共変量シフト、転移学習、など）をグラフィカルモデルで表現し、それらに対して有向分離を適用してみたいと思います。

 

[続き・関連]

machine-learning.hatenablog.com

今回の記事がよくわからん！という方には，次のような入門書もあります．

books.rakuten.co.jp

*1:$y$が連続値を取る場合は和$\sum_y$の代わりに積分$\int dy$を使えばOKです。

*2:このような確率モデルの表記の仕方はベイジアンネットワークとも呼ばれます。ちなみに考案者である計算機科学者のJudea Pearlは2011年にこの功績によってチューリング賞を受賞しています。

*3:ちなみに矢印の根元にあるノードは先にあるノードに対して親であると言います。逆は子です。この場合は例えばAがBの親であるとか、CがBの子であるとかって言ったりします。祖先や子孫も直感どおり定義されます。

*4:変分近似の基礎 

http://machine-learning.hatenablog.com/entry/2016/01/23/123033

*5:MCMCと変分近似の比較 

http://machine-learning.hatenablog.com/entry/2016/02/04/201945

もうバグに悩まされることもない？MITの研究者が人工知能を利用した自動デバッグシステムを開発

一般の方向け

こんにちは。

MITの研究者が従来法よりも10倍多くのバグを修正できるアルゴリズムを開発したそうです。

news.mit.edu

 

・従来法の問題点

ソースコードのバグを自動修正するという研究は従来からありました。一般的な方法としては、修正したいソースコードに対する正解セット（入力値とそれに対する正しい出力値）をいくつか人間が用意してあげて、その正解セットに合致するような修正提案をシステムが一生懸命探すというものです。このような手法は論理的な計算を多く必要とするので時間がかかるのと、結局修正コードを作ってもらっても与えたセット以外の入力に対してめちゃくちゃな値を出して使えないとかいった問題がありました。

 

・大量のパッチからプログラムの修正パターンを学習

今回のMITの研究者が開発したアルゴリズムの革新的なところは、ソースコードの修正に機械学習技術*1を利用した点です。研究者らは、GitHubから大量のオープンソースプログラムの修正パッチを取得し、それを「学習データ」としてコードを自動修正するための汎用的な規則を抽出しました。機械学習アルゴリズムを使うには、生データ（今回はソースコード）に対してどのような特徴量を設計したらいいのかがひとつの重要なポイントになります。この研究ではソースコード上の変数にいくつかの特性（変化する値か定数か、グローバルかローカルか、など30種類）を与えることによって特徴量を設計しているようです。この特徴量の空間でバグの入ったコードと修正パッチの規則性を学習します。従来技術では1個か2個ほどのバグしか修正できなかったのに対して、今回の手法は15から18個ものバグを修正できたそうです。

 

・これからの課題と雑感

今のところはソースコード全体に影響を及ぼすような複雑なバグは修正できず、ローカルな一対一対応のような小さなバグを修正するのみとなっているようです。とはいえ、それでも人間のかなりの作業量を減らせることに間違いはありません。また、アルゴリズムの学習データとなるソースコードは日々オープンに蓄積されていきますし、今回の技術もまだまだ洗練されているとは言えないので、これからの技術改善に注目です。

 

*1:「人工知能」は人間などの「知能」をコンピュータ上に実現するための技術の総称です。それに対して「機械学習」はもうちょっと工学寄りで、データから規則的な構造を自動発見して未来の予測や判断を行うための技術の総称です。