MLPシリーズ「ベイズ深層学習」概要まとめ
今回は8月に出版した講談社機械学習プロフェッショナルシリーズの「ベイズ深層学習」の概要を書いてみます. www.kspub.co.jp 講談社のページ等では目次は載っていますが,それより詳細な情報はネットにはないので,もう少しだけ踏み込んだ内容をここで紹介することにします.
内容紹介
第1章 はじめに
ベイズ統計と深層学習(ディープラーニング)は仲が悪いように世間的には見られがちですが,実は両者は非常に親和性が高いことを解説しています. 両分野のそれぞれの利点としては,ベイズ統計ではモデルの高い解釈性や設計の明確さ,深層学習ではGPUなどを用いた大規模データの効率的な計算方法等を挙げることができます.これらの利点は相補的であり,組み合わせることによってアルゴリズムの改善が期待できます. また,両分野には共通点もあります.深層学習ではタスクごとにネットワーク構造を設計する必要性がありますが,これはベイズ統計におけるモデリング作業と本質的に一致しています.つまり,両分野においてもデータ・タスクに合わせたモデル設計の重要さが認識されていると言えます.
本書は単なる「ニューラルネットワークのベイズ的な取り扱い法」や「最新の深層学習技術のガイダンス」といったものではありません.本書は「複雑な統計モデルの設計法とそれに対する効率的な確率推論手法」という大きな枠組みの中で,重要な分岐点となった技術を系統立てて紹介する内容になっています.
第2章 ニューラルネットワークの基礎
ここでは最もシンプルな統計モデルである線形回帰モデルから出発し,ニューラルネットワークの成り立ちや利点などを解説していきます. 学習方法も最小二乗法から,誤差逆伝播法を使った基本的な最適化手法まで解説します. また,画像認識で飛躍的な精度向上を果たした畳み込みニューラルネットワークなどの典型的なモデル例なども紹介します.
第3章 ベイズ推論の基礎
ベイズ推論の超基本的なところを解説します.基本的な確率計算から,指数型分布族といったベイズ統計における重要な構成要素,さらに線形回帰に対する利用例を示します.また,気になる人向けに最尤推定や正則化学習との理論的な関係性に関しても簡単に説明します. このあたりの話は,下記の「ベイズ推論による機械学習入門」も併せて読むと理解が深まります. www.kspub.co.jp
第4章 近似ベイズ推論
ここからだんだん本題に入っていきます. 近年ベイズ統計を実用レベルまでに一気に押し上げたのは,変分推論法を始めとしたいくつかの近似推論手法の開発によるものです. 特に,「ベイズ推論による機械学習入門」ではあまり説明されなかったハミルトニアンモンテカルロ法やモーメントマッチング法,期待値伝播法など,ニューラルネットワークに適用できる種々の計算手法も紹介します.
第5章 ニューラルネットワークのベイズ推論
ここでは第2章で紹介したニューラルネットワークを確率モデルとして解釈しなおし,確率的な推論計算によって学習・予測する方法を紹介していきます.特に,第4章で解説した近似推論手法を次々にベイズニューラルネットワークモデルに適用していきます.
また,ここでは深層学習の研究領域でこれまでに開発されたドロップアウトや確率的勾配降下法などの効果的な計算手法が,実は変分推論法を始めとしたベイズ統計の方法論として解釈しなおせることを示します.その結果を利用することにより,ベイズ統計の利点を生かして予測の「不確実さ」を簡単に示せるようなテクニックや,それを使った強化学習などへの応用事例なども数多く紹介します.
第6章 深層生成モデル
ここでは特に深層生成モデルに着眼して,ベイズ統計と深層学習の関係性について見ていきます. 変分オートエンコーダー(VAE)や敵対的生成ネットワーク(GAN)は深層学習の分野において非常に人気のある深層生成モデルです.VAEに関しては,「生成ネットワークによるデータの生成過程のモデル化」と「識別ネットワークによる近似ベイズ推論の効率化」という観点で解釈を試みます.GANに関しては,変分推論法,近似ベイズ計算(approximate Bayesian computation, ABC),密度比推定といった技術を組み合わせによってベイズ的な学習手法として解釈することができます.
また,ベイジアンノンパラメトリクスの技術を使うことによって,ニューラルネットワークに対して無限の深さ,無限の隠れ層数を仮定したモデルを構築することができます.これを使って,ニューラルネットワークの構造をデータから自動的に決定する手法も紹介します.
第7章 深層学習とガウス過程
近年注目を集めているガウス過程と深層学習との関係性に関して解説します. ガウス過程は関数上の確率分布です. 前半ではガウス過程自体の簡単な紹介にフォーカスし,特にガウス過程も深層学習と同様,大量のデータを短時間で効率的に学習できるような手法が存在することを示します. ガウス過程に関しては,同シリーズの下記入門書がお勧めです. www.kspub.co.jp
後半では,隠れ層を無限大に拡張した場合のニューラルネットワークがガウス過程として解釈できることを示し,行列計算によって解析的に厳密な予測が実行できることを示します.ReLUなどのよく使われる非線形関数を持つニューラルネットワークモデルの,カーネルによる表現なども詳細な計算付きで解説します. また,ガウス過程の教師なし版であるガウス過程潜在変数モデル(Gaussian process latent variable model)も紹介し,さらにそれらを複数重ねた深層ガウス過程(deep Gaussian process)といったモデルも紹介します.
その他
想定する読者層
前著と比べてこの辺の定義は結構難しく,人それぞれといった感じです. 単純に言えば,ベイズ統計学と深層学習のどちらかに興味を持った(比較的数学力強めな)人には全員お勧めできると思います. 読むためにはどちらか一方の知識を持っているか,あるいはどちらもそこそこの知識を持っている必要があると思います. ベイズ統計に詳しい方には,ディープニューラルネットワークといったとてつもなく複雑で巨大な問題にどうやって立ち向かっていくか,といった観点で面白いと思います.実際,このような複雑な確率モデルを上手に設計し,大量データを投入して効率良い推論していくのはベイズ統計の中心的な研究課題です. 深層学習に詳しい方は,過剰適合とかパラメータチューニングの難しさ,解釈性の困難さや不確実性の表現能力など,深層学習の数々の問題点を解決する手段として参考になると思います.また,深層学習の数多くの納得感のないモヤモヤした方法論に一定の解釈を与えるなどの目的としても本書は使えます.また,ベイジアンノンパラメトリクスを使った構造の自動決定やガウス過程との関連は今後大きなトレンドになる可能性が高いと思われます.
大変だったこと
ベイズx深層学習という2つの大きなテーマを相手にすると,とにかく参照すべき論文数が膨大になります.ただの最新技術紹介になるのを防ぐため,前著同様,「モデルx確率推論」という一定のスタンスを保ちながら内容を整理・厳選しています.結果として,1980年代から2019年の最新のものまで,重要と思われる研究成果をフラットに紹介しています.執筆には概算で2000時間くらいかかっています.
協力してくださった方
深層学習から見ても,ベイズから見ても,なるべく正確な内容になるようにしたかったので,今回は両分野で最強レベルの研究者の方に内容チェックをお願いしています.この場を借りて厚く御礼申し上げます.
線形回帰を1つ1つ改造して変分オートエンコーダ(VAE)を作る
こんばんは.
今日は統計や機械学習において最も基本となる手法である線形回帰から出発し,1つ1つモデルや学習方法に変更を加えていき,最終的に深層学習の分野で非常に良く使われている生成モデルである変分オートエンコーダ(variational auto-encoder,VAE)*1*2を導いていきたいと思います.
2014年に発表されたVAEは,勾配近似を得るためのreparametrization trickや,効率的に潜在変数を近似推論する認識モデル(recognition model, inference model)の導入,確率的勾配法(stochastic gradient descent,SGD)の2重適用など,様々なアイデアが散りばめられている確率的生成モデルです.背景としては,当時ニューラルネットワークを用いて画像を生成するといったアプローチが(CNNを使った識別などと比べて)それほどメジャーではなかったこと,またニューラルネットワークに対して変分推論(variational inference)を適用する事例もそれほど多くなかったことがブームのきっかけになったのではないかと推察しています.
生成モデルや変分推論に詳しくない方は,VAEの論文を読んで「てんこ盛り」感があるように思えるかもしれないですが,1つ1つの要素を分解して考えてみればどのような必然性を元にVAEが構成されているのかを知ることができます.具体的には,線形回帰モデルに対して次のような近似推論の導入とモデルの拡張を施せばVAEが得られます.
個人的には,最先端の「全部載せ」アルゴリズムをただ漫然と受け入れるのではなく,個々の要素の必然性を理解することが機械学習エンジニアの技術力につながってくると思っています.逆に言えば,この記事によって「俺の課題,VAEじゃなくてPCA(主成分分析)で十分じゃん!」みたいになってくれれば大成功です.
線形回帰
Zを入力データセット,Xを出力データセット,Wをこのモデルのパラメータであるとします.これらの同時分布を次のようにモデル化します.
 ただし,p(Z)はZの事前分布で,各潜在変数z_nに対して次のような等方ガウスを使うことにします.
ただし,p(Z)はZの事前分布で,各潜在変数z_nに対して次のような等方ガウスを使うことにします.
 観測モデルp_w(X|Z)は次のような線形性を仮定します.
観測モデルp_w(X|Z)は次のような線形性を仮定します.
 ここでは,計算の簡便性からガウス分布Nを観測分布として採用しており,λはその精度パラメータ(分散の逆数,今回は学習せず固定)です.
式(3)のパラメータWを尤度最大化(最尤推定)で学習することにすると,
ここでは,計算の簡便性からガウス分布Nを観測分布として採用しており,λはその精度パラメータ(分散の逆数,今回は学習せず固定)です.
式(3)のパラメータWを尤度最大化(最尤推定)で学習することにすると,
 と書けます.せっかく設定した事前分布p(Z)ですが,結果的にWの学習に何の影響も与えないことがわかりますね.
尤度が最大となるWは
と書けます.せっかく設定した事前分布p(Z)ですが,結果的にWの学習に何の影響も与えないことがわかりますね.
尤度が最大となるWは

を解くことによって次のように解析的に求められます.

あとは新規の入力データz_testに対する未知の出力値x_testを次のように点として予測するのが一般的です.

線形次元削減(確率的主成分分析)
さて,先ほどとまったく同じモデルを使い,今度はZが観測できないようなシチュエーションを考えてみます.つまり,Zを潜在変数として取り扱います.この場合,最尤推定を実施するためには次のようにZを周辺化した上でWに関して尤度最大化を行わなければなりません.
 式(9)は残念ながらWに関して解析的に最大値が求められないことが知られています.ここでは次のようなEMアルゴリズムによる繰り返し最適化を用いて,尤度の局所的な最大値を求めることにします*3.
式(9)は残念ながらWに関して解析的に最大値が求められないことが知られています.ここでは次のようなEMアルゴリズムによる繰り返し最適化を用いて,尤度の局所的な最大値を求めることにします*3.
<E-step>

<M-step>

iは最適化の繰り返しのインデックスです.EMアルゴリズムの詳しい意味に関してはPRMLなどをご参照ください.
このモデルでは,各E-stepおよびM-stepは解析的に実行することができます.E-stepでは,パラメータWを固定した上でのZの事後分布は

とガウス分布で表すことができます.一方,M-stepはパラメータWで微分すれば線形回帰とほとんど同じ計算により

と解析解が求められます.
ところで,このような主成分分析(PCA)でもVAEのように画像を生成したり,次のように欠損値を補完したりすることができます.

また,モデルに対してちょこっとだけ変更を加えれば次のようなモザイク除去も作ることができます.

このように,単純な確率的主成分分析を使いこなすだけでも本質的にVAEなどの深層生成モデルでやられていることは実現できます.もちろん,データが大量にある場合や,データが高度に非線形な構造を持っていると思われる場合は,VAEをはじめとしたフレキシブルなモデルの方が性能が良くなります.
ミニバッチ化
先ほどのEMアルゴリズムをミニバッチで学習できるように変更しましょう.これにより,メモリ効率はもちろん,学習の効率性も上がることが知られています.いくつかやり方がありますが,ここではstepwise EM*4というシンプルでメモリ効率の良い手法を使います.
簡単のため,データセットからランダムに1つのデータx_nを取ってくることにします.E-stepでは,パラメータWを固定した上で,1つのデータx_nに対する事後分布のみを推論してあげればよく,
<E-step>

となります.ここで計算した事後分布による期待値を次のようにM-stepのパラメータ更新で使います.
<M-step>

ここでη_iはステップサイズです.イメージとしては,ひとつ前のステップiまでに学習されたパラメータの値W(i)を保ちつつ,ステップi+1で新しい更新量を重み付きで加えてあげる感じです.
また,同様の考え方は完全なベイズ版であるstochastic variational inference*5にも利用されています.
非線形関数の導入
次にモデルに非線形関数を導入してみましょう.ちょっと深層学習っぽくなってきますね.次のように,p(X|Z)に対して,パラメータθに関して微分可能な非線形関数f_gを導入します.

非線形関数としては,例えば次のように単純にtanhを導入し,

としても良いですし,非線形関数を再帰的に適用してもっと深い層を考えてあげても良いです(ここではθ={W, b}としています). さて,ここで生じる問題点としては,非線形関数f_gを導入したことにより,E-stepおよびM-stepがそれぞれ解析的に計算できなくなってしまうことです.したがって,それぞれのstepで勾配を利用した最適化を導入することにします. まず,E-stepですが,解析的に簡単な分布(前の例ではガウス分布)が導出できないので,事後分布がガウス分布であると無理やり仮定し(=近似する事後分布のクラスを制限する),その中でKLダイバージェンスがなるべく小さくなるように調整します.つまり,まずz_nに対する近似分布を

と置きます.ここでφ_n={μ_n,σ_n}は変分パラメータと呼ばれます.さらに,次のように確率的勾配法によりKLダイバージェンスを小さくするように変分パラメータを更新します.
<E-step>
 α_Eはステップサイズです.実はこの勾配計算もまだ解析的には実行することが出来ません.というのも,式(21)のKLダイバージェンスの項を書き下してみると,
α_Eはステップサイズです.実はこの勾配計算もまだ解析的には実行することが出来ません.というのも,式(21)のKLダイバージェンスの項を書き下してみると,

となり,式(22)の第1項に非線形関数f_gを含んだ複雑な期待値計算が現れてしまいます.
ここでは解析的に積分を実行し期待値を計算することは諦め,z_nを1つサンプルすることにより近似的に期待値を求めることにします.z_nをそのままサンプルしてしまうと,式(22)の第1項目が変分パラメータφ_nの関数でなくなってしまうので,後で変分パラメータの勾配が計算できません.これを解決する方法はいくつかありますが,VAEの元論文で使われているのはreparametrization trickと呼ばれている手法で,次のように変数変換を行ったうえでz_nをサンプリングすることにします.

こうすることにより,微分対象となる変分パラメータのないq(ε)の分布に対する期待値を取っていることになり,サンプリングで積分を近似した後に変分パラメータφ_nに関して微分ができるようになります.
M-stepはもう少しシンプルで,単純にz_nをサンプルしたあとにθで微分すれば勾配が求まります.
<M-step>

ここで式(26)における負の対数尤度は,ニューラルネットワークにおける誤差関数と等価であり,通常の合成関数の微分で勾配が計算できます(誤差逆伝播法,backprop).
認識モデルの導入
VAEの元論文では,上記のミニバッチを使ったE-stepの更新をより効率化するために,次のようなニューラルネットワークを使った認識モデル(recognition model)*6を提案しています.

ここではμやσは一時的に置かれている変数に過ぎず,新しく導入した非線形関数f_rの出力になっています.先ほどの例だと,1つのデータ点x_nに対して潜在変数z_nの近似事後分布を1つ1つ最適化しなければならなかったのですが,変分パラメータφ={W,b}を使った非線形関数を使うことにより,異なる複数のデータ点に対しても対応するzの近似事後分布が更新されるようになります.これは,似たような入力xに対しては似たような潜在変数zの事後分布になるはず,というヒューリスティクスから由来しています(amortized inference*7).これにより収束の高速化を狙おうというのがここでの認識モデル導入の狙いです.「変分パラメータが複数のデータ点にわたってシェアされている」と元論文では説明されています.
認識モデルを導入することにより,変分パラメータの最適化にも誤差逆伝播法を適用する必要が出てきます.E-stepにおける式(21)のKLダイバージェンスの項は,今回の認識モデルを用いた場合は次のようになります.

ここでz_nは先ほどと同様,reparametrization trickを使います.式(29)の最後の項はニューラルネットワーク(非線形関数)ですので,通常の誤差逆伝搬によりφに関する勾配が計算できます.
今回は,統計学や機械学習における最も基本的な予測モデルである線形回帰に対して1つ1つ変更を施していき,深層生成モデルとして有名な変分オートエンコーダの成り立ちを確認してみました.1つ1つの技術はそれなりに必然性を持って導入されているものであり,逆に言えばデータ数の多くない場合やデータの複雑な非線形構造を抽出する必要がない場合は最も単純な潜在変数モデルである線形次元削減でも十分であることも説明しました.
ちなみに今回の記事はすべてパラメータを確率変数として扱っていない非ベイズのアルゴリズムになっています*8.今回紹介したアルゴリズムはあくまで解説目的であり,実際はパラメータに対する正則化項を付け加えたMAP推定版にしたり,パラメータの事後分布も考慮するような完全な近似ベイズ推論の枠組みで実装するのが理想です(議論の大筋は今回と変わりません).
モデルの拡張は実はこれで終わりではありません.前回の記事(深層学習はガウス過程)でも解説しましたが,ニューラルネットワークにおける重みパラメータの数を無限大にしてあげるとガウス過程に一致します.今回のVAEの場合でも,非線形関数f_gの重みパラメータを無限大に増やすことにより,ガウス過程潜在変数モデル(Gaussian process latent variable model, GPLVM)*9と呼ばれるより洗練されたモデルを得ることができます.
今回のようなベイズ推論と深層学習の融合領域に関しては次の書籍が詳しいです. www.kspub.co.jp
線形回帰,潜在変数モデル,変分推論,ベイズニューラルネットの推論等は下記書籍に基本的な解説があります. www.kspub.co.jp
*1:https://arxiv.org/abs/1312.6114
*2:https://arxiv.org/abs/1401.4082
*3:https://rss.onlinelibrary.wiley.com/doi/abs/10.1111/1467-9868.00196
*4:https://cs.stanford.edu/~pliang/papers/online-naacl2009.pdf
*5:http://www.columbia.edu/~jwp2128/Papers/HoffmanBleiWangPaisley2013.pdf
*6:変分推論における事後分布に対する近似分布の表現手段を表しており,推論モデル(inference model),変分モデル(variational model)とも呼ばれます.要は「凝った近似分布」です.
*7:https://web.stanford.edu/~ngoodman/papers/amortized_inference.pdf
*8:したがって元論文で言われているauto-encoding variationa Bayesはベイズではありません.ただし,full Bayes版はappendixにちゃんと載っています.
*9:http://proceedings.mlr.press/v9/titsias10a/titsias10a.pdf
深層学習はガウス過程
おつかれさまです. 僕はあまり深層学習に関して記事を書くことはないのですが,ちょっと気になった論文があったので紹介します.
[1711.00165] Deep Neural Networks as Gaussian Processes
論文はGoogle Brainの研究者らによるもので,NIPS2017 Bayesian Deep Learning WorkshopICLR2018にacceptされています.実は深層学習をガウス過程(Gaussian process)で構築するのはこの論文が初出ではないのですが,論文ではベイズ学習,深層学習,カーネル法を簡略かつ包括的に説明している内容になっているので非常に参考になります.
さて,「深層学習はガウス過程」というのはちょっぴり宣伝的なタイトルにし過ぎてしまったのですが,もう少しだけ正確に論文の要点をまとめると次のようになります.
- 背景
- やったこと
今回の記事では,ガウス過程の基礎から論文の内容までをざっくり説明したいと思います.
ベイズ線形回帰からガウス過程まで
簡単に言うと,ここから紹介するガウス過程とはノンパラメトリックな回帰モデルです.
まず始めにベイズ線形回帰から始めてガウス過程の成り立ちを説明しようと思います.
線形回帰モデルでは,実数の出力値は,入力値
,
次元への特徴量変換を行う関数
,パラメータ
を使って次のように生成されると仮定します.
 ここでλは観測に対する固定の精度パラメータです.
また,パラメータ
ここでλは観測に対する固定の精度パラメータです.
また,パラメータに仮定する事前分布として次のようなガウス分布を置きます.
 ここで
ここでは
x
の精度行列です.
学習用に
組の入出力データ
が与えられたとき,新規のテスト入力
*に対する出力
*の予測分布は,次のようにパラメータ
を事後分布で周辺化することによって得ることができます.
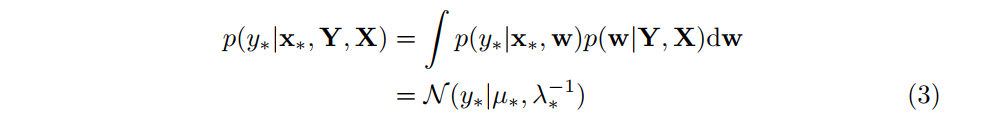 ただし,ガウス分布の平均と精度は次のようになります.
ただし,ガウス分布の平均と精度は次のようになります.
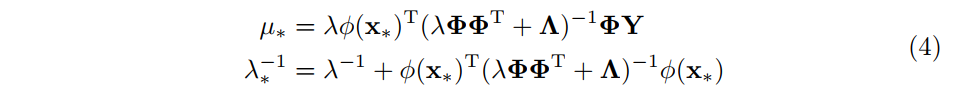 詳細な計算方法に関しては拙著にまったく同じものが載っているのでよかったらご参考ください.
詳細な計算方法に関しては拙著にまったく同じものが載っているのでよかったらご参考ください.
さて,式(4)の予測平均と予測分散を次のように書き直してみます.
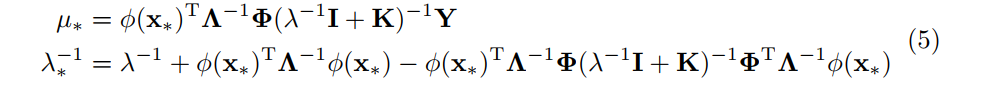 ただし,
ただし,
 と置きました.また,大文字の
と置きました.また,大文字のは
x
の行列であり,各
成分が
の
次元目の値を表しています.
ここでは行列のinverse lammaを使って式変形を行っています1.
式(5)および式(6)の結果を見てみると,特徴量関数
は常に
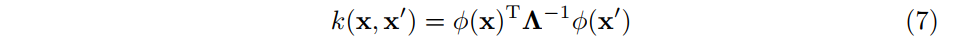 のような形に集約されていることがわかります.
のような形に集約されていることがわかります.をカーネル関数または共分散関数と呼びます.これはつまり,特徴量抽出を行う関数
を設計するのではなく,共分散関数
を直接設計することによっても回帰が行えることを示しています.共分散関数は2つの入力点に関する相関を定義するものであるため,ある意味異なるデータ間の類似度のようなものを設計しているとも言えます.また当然ですが,共分散行列はガウス分布の共分散なので正定値である必要があります.
共分散関数の選択
さて,具体的な共分散関数にはどのようなものがあるのでしょうか.ガウス過程で最もよく使われている共分散関数の1つに,次のような指数2次カーネル(exponentiated quadratic kernel)と呼ばれるものがあります(RBF kernel, squared exponential kernel, gaussian kernelなどと呼ばれることもあります).
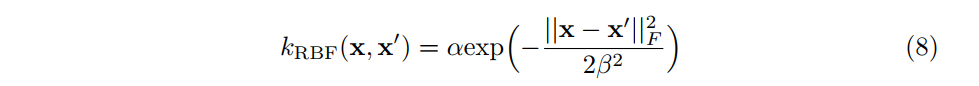
,
はこの共分散関数のパラメータです.ガウス分布と同じ関数の形をしていますが,これはただ単にたまたまであり,ガウス分布のように正規化されている必要はありません.ちなみにこの共分散関数に対応する特徴量
というのも実は存在しており,無限次元の特徴量抽出になります2.
さて,式(8)で表される共分散関数以外にも多くのものが提案されています.ニューラルネットに関連するものであれば,次のような無限ユニット数を持つERFやReLUといった非線形関数に対応した共分散関数が存在します.
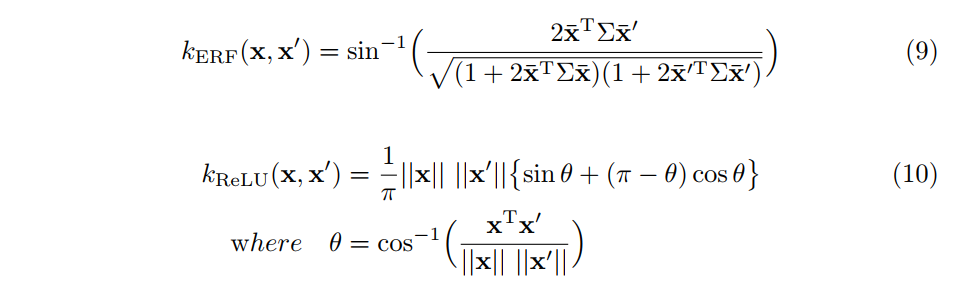 また,複数の共分散関数を足したり掛けたりして組み合わせることによって新しい共分散関数を構築することも可能です3.
また,複数の共分散関数を足したり掛けたりして組み合わせることによって新しい共分散関数を構築することも可能です3.
いくつかの(解析的に計算できる)共分散関数に対して,単純な一次元の回帰を行ってみたのが次のアニメーションです.上段はそれぞれの事前分布からサンプルされた関数の例で,下段は順次データ点を与えていった場合の予測分布の推移を示しています.
 左から順に,多項式関数(3次関数),RBFカーネル,ニューラルネット(ERF),ニューラルネット(ReLU),ディープニューラルネット(ReLU)です.最後のディープに対する共分散関数の構成方法に関しては次の節で解説します.
左から順に,多項式関数(3次関数),RBFカーネル,ニューラルネット(ERF),ニューラルネット(ReLU),ディープニューラルネット(ReLU)です.最後のディープに対する共分散関数の構成方法に関しては次の節で解説します.
また,この結果を生成するコードは下記Githubに置きました.コアな部分は20行程度です. https://github.com/sammy-suyama/MLBlog/blob/master/src/demo_GPDNN.jl
ガウス過程としての深層学習
さて,ここからは本題である深層学習モデルの共分散関数の導出に関して見ていきましょう.
まず,非線形変換が1層だけのニューラルネットワークの回帰モデルを考えてみます.
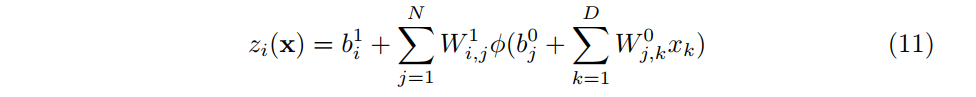
は
次元目の入力データの値で,
は
番目の出力です.
や
はネットワークのパラメータであり,各要素が次のような1次元の独立なガウス分布に従って生成されていると仮定します.
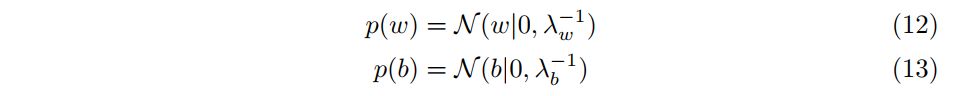 各パラメータが独立なので,異なる
各パラメータが独立なので,異なる個の
も独立に値が決定されることになります.
ここで,隠れユニットの数
を無限にしたらどうなるでしょうか.ここでは
はもはや何の確率分布に従っているかは不明ですが,各
は独立であることがわかっているので,無限に足し合わせれば中心極限定理によりガウス分布に近づいていくことになります.最後に足される
もガウス分布に従うので,結果として出力
もガウス分布に従うことになります.
したがって,非線形関数に関する共分散を期待値を使って書けば,
は次のような共分散関数を持つガウス過程として表せます.
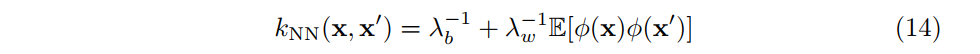 この議論は一般的なL層のモデルに拡張しても成り立ちます.ある
この議論は一般的なL層のモデルに拡張しても成り立ちます.ある層目の出力がガウス過程に従うならば,次の
層目の共分散もガウス過程に従うので同様にして共分散関数を計算できるわけです.この関係性を書いてみると,
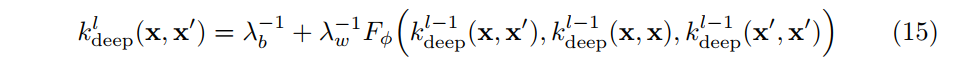 となります.
となります.は
層目の非線形変換
から決定的に求められます.
具体的にReLUを非線形関数として選んだ場合の再帰式は次のようになります.
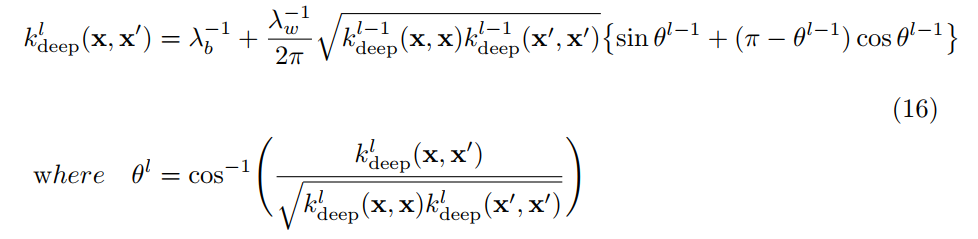 このカーネルを計算し,あとは一般的なガウス過程の予測の式(5)に入れて計算すれば,基本的には行列演算のみで深層学習のベイズ予測ができることになります.
このカーネルを計算し,あとは一般的なガウス過程の予測の式(5)に入れて計算すれば,基本的には行列演算のみで深層学習のベイズ予測ができることになります.
下記の図は論文で示されている実験結果の1つです.
 横軸は予測分布が出力した分散で,縦軸はテストデータにおける二乗誤差です.図からわかるように,予測分散が大きくなるにつれて,テスト誤差も大きくなっていく傾向が見て取れます.すなわち,「予測に自信がない(=分散が大きい)場合は,実際に予測の間違えも大きくなっている」ということになります.
これはベイズ学習を深層学習に用いた場合のもっとも重要な利点です.残念ながら現在の機械学習の評価方法は専ら予測誤差を使って精度評価のみを行うという慣習がついてしまっており,不確かさを表現できることの重要性が軽視されがちです.しかし,このような予測の不確かさの定量化は,少ないデータで効率良く学習したり,「過剰な自信」による誤判断を未然に防いだりすることができます.これが(深層学習に限らず)機械学習モデルをベイズ化することが,自動運転などのアプリケーションに重要であると考えられている所以です.また,環境を学習しながら報酬を最大化していくような強化学習などの枠組みでは,このような不確かさの定量化が効率的な探索を行う(explorationとexploitationのトレードオフを取る)ために不可欠になってきます.
横軸は予測分布が出力した分散で,縦軸はテストデータにおける二乗誤差です.図からわかるように,予測分散が大きくなるにつれて,テスト誤差も大きくなっていく傾向が見て取れます.すなわち,「予測に自信がない(=分散が大きい)場合は,実際に予測の間違えも大きくなっている」ということになります.
これはベイズ学習を深層学習に用いた場合のもっとも重要な利点です.残念ながら現在の機械学習の評価方法は専ら予測誤差を使って精度評価のみを行うという慣習がついてしまっており,不確かさを表現できることの重要性が軽視されがちです.しかし,このような予測の不確かさの定量化は,少ないデータで効率良く学習したり,「過剰な自信」による誤判断を未然に防いだりすることができます.これが(深層学習に限らず)機械学習モデルをベイズ化することが,自動運転などのアプリケーションに重要であると考えられている所以です.また,環境を学習しながら報酬を最大化していくような強化学習などの枠組みでは,このような不確かさの定量化が効率的な探索を行う(explorationとexploitationのトレードオフを取る)ために不可欠になってきます.
論文には他にも計算効率の良い共分散の構成方法や,超パラメータに関する相転移の解析などが含まれており,そちらも大変興味深いです.今回の記事ではガウス過程と深層学習の関係性に注目したかったので割愛します.
所感と今後
ガウス過程で解釈することの利点
深層学習を共分散関数の中で表現し,ガウス過程として解釈する有用性はざっくり挙げるとすれば次のようにまとめられるでしょう.
- 原理的に過学習をしない
- 予測の不確実性を出力できる
- 共分散関数を自動的に最適化・選択できる
1と2はベイズ推論から来る当然の特性です.3に関しては,深層学習におけるネットワークの構造や非線形変換の自動学習を行っていることに対応するでしょう.現在はガウス過程を使って既存の深層学習の超パラメータを調整する方法(ベイズ的最適化)が流行っていますが,皮肉にも深層学習自体をガウス過程にしてしまった方が手っ取り早いということになりますね.
また,これらに付随して,モデルのデザイン性や解釈性に関しても今後は重要になるでしょう.Oxford大学教授でDeepMindのリサーチャーであるTeh先生は,NIPS2017の講演で「解釈のできないパラメータ空間ではなく,関数空間で考えよう」と言っています.
www.youtube.com このように,これからは深層学習をベイジアンノンパラメトリクスの文脈で組みなおす研究が増えてくるんじゃないかと思っています.
ガウス過程で解釈することの課題点
ところで,ガウス過程にしてしまうことで課題点もあります. 1つは,隠れユニットの数を無限にしてしまうと,出力の各次元が統計的に独立になってしまうことです.これにより,ニューラルネットワークに特有の「中間層で特徴量を表現する」みたいなことが原理的にできなくなります.ただし,論文では無限の中間層を持つガウス過程が伝統的な深層学習よりも実験的に良い結果を示しているので,この議論自体に意味があるかは疑問の残るところです.
これに関連する課題として,実はこちらの方が重要なのですが,出力が独立になってししまったことにより,多次元回帰やマルチタスク学習が原理的に行えないことが挙げられます.しかし,後述しますが,ガウス過程の研究では出力の次元間に関して相関を導入できる方法がすでにいくつか存在しています.
関連研究メモ
さて,他にも個人的に気になるガウス過程や深層学習の関連研究を思いつくまま並べておきます.
1.畳み込みモデル,時系列モデル
最新の論文ですが,畳み込みニューラルネット(convolutional neural network)のような構造をガウス過程に取り込む研究があります.
[1709.01894] Convolutional Gaussian Processes
また,LSTM(Long short-term memory)の出力をガウス過程の入力に使うような話もあります.
[1610.08936] Learning Scalable Deep Kernels with Recurrent Structure
2.カーネル関数の最適化や自動選択
興味深い事例として,与えられたデータに対してガウス過程のカーネル関数(共分散関数)を自動探索し,解析結果を自然言語で説明するようなシステムが考案されています.
Automatic Construction and Natural-Language Description of Nonparametric Regression Models
3.能動学習および強化学習
ベイズ推論を使えば不確実性に基づいて環境を探索できるので,直接強化学習の問題に応用することができます.
PILCO: A Model-Based and Data-Efficient Approach to Policy Search
4.マルチタスク学習
ガウス過程の出力ベクトルの次元間に相関を持たせる方法はいくつか提案されています.
Efficient Multioutput Gaussian Processes through Variational Inducing Kernels
5.潜在変数モデル
ガウス過程にはGPLVM(Gaussian process latent variable models)と呼ばれる潜在変数モデル版も存在します.GPLVMに今回のようなdeepなカーネルを使えば,VAE(variational auto encoder)などとは別の深層生成モデルが作れることになりそうです.
Bayesian Gaussian Process Latent Variable Model
また,通常のGPLVMをスタックする(GPの出力を別のGPの潜在的な入力にする)ことによって,deepなガウス過程を構成することもできます.
このような構成方法であれば,低層で抽出された潜在構造を次の層へシェアすることができます. 論文では「150個のデータに対して5層が最適」のような推定もできており,小規模データでも過学習しないベイズの強みが理解できますね.
6.スケーラビリティ
ガウス過程の最大の課題は大規模データに対するスケーラビリティです.まともに予測分布を計算しようとすると,データ数をNとしたときO(N3)の計算時間がかかってしまうため,普通にやるとビッグデータの時代には使い物になりません.幸いなことに,これまでに数多くの近似推論手法が開発されてきています.中でも有望なのが本ブログでも何度か紹介している変分推論法(variational inference)です.下記の論文で変分法を用いてガウス過程をスケーラブルにするテクニックが網羅的に紹介されています.
Scalable Gaussian Process Inference using Variational Methods
今後も深層学習と近似ベイズ推論の両研究分野で技術的な輸出入が起こると思います.いろいろな手法の理論的な一致や拡張・一般化が見られると面白そうですね.
7.ガウス過程以外を使う
例えばStudentのt過程は,ガウス過程と同じような特性を持ち合わせていながら,外れ値に頑強であるという特徴を持つので,これをディープなモデルに対して使ってみても良いかもしれません.
Student-t Processes as Alternatives to Gaussian Processes
基礎を知りたい方
最後になってしまって申し訳ないですが,今回の記事の内容を理解するために必要な基礎理論を解説した教科書・資料や,古典的な論文等を紹介しておきます.
Gaussian Process for Machine Learning
http://www.gaussianprocess.org/gpml/
Carl Edward Rasumussen先生によるガウス過程の教科書の決定版です. 2006年なのでちょっと古くなってきてしまいましたが,ガウス過程による回帰・分類はもちろん,共分散関数の構成法,モデル選択,大量データに対する近似学習法まで網羅しています.SVMなどの類似手法との関係性も解説しています.
Bayesian Learning for Neural Networks
http://www.springer.com/jp/book/9780387947242
1996年に執筆されたRadford Neal先生の伝説的論文ですが,高い先見性と深い洞察に驚かされます.ベイズニューラルネットのハミルトニアンモンテカルロによる学習のほか,本記事で解説したニューラルネットとガウス過程の関係性もここで解説されています.事実,近年の機械学習におけるガウス過程のブームはここから始まりました.また,無限に深くした場合のニューラルネットの挙動に関しても考察があります.
ガウス過程の基礎
日本語の解説スライドはこちらです.非常にわかりやすくまとめられています.
松井先生:
http://www.ism.ac.jp/~daichi/lectures/H26-GaussianProcess/gp-lecture1-matsui.pdf
持橋先生:
http://www.ism.ac.jp/~daichi/lectures/H26-GaussianProcess/gp-lecture2-daichi.pdf
ベイズ深層学習の入門書
今回のようなベイズ推論と深層学習の融合領域に関しては次の書籍が詳しいです. www.kspub.co.jp
ベイズ学習の基礎
拙著です.
ベイズ推論による機械学習入門 機械学習スタートアップシリーズ | 書籍情報 | 株式会社 講談社サイエンティフィクwww.kspub.co.jp
データに欠損がある場合の教師あり学習
おはようございます.
今回は教師あり学習モデルを題材に,入力データが欠損している場合のベイズ流の対処法を解説します.ベイズモデルというと,たいていの場合は事前分布の設定の仕方云々だとか,過学習を抑制できるだとかに議論が注目されがちですが,個人的には,パラメータや潜在変数を推論することとまったく同じ枠組みで欠損値も同時に推論できることが,実用上非常に便利なベイズの特性だと思っています.
データの欠損部分の取扱い
データに欠損部分が存在することはよくあります.センサーデータを解析する際は,ネットワークの状況やデバイスの不具合によってデータの一部が欠けた状態で上がってくることがあります.スマホから複数種類のデータを集めるといった状況を考えてみると,例えば加速度センサーの値は継続的に取得できたとしていても,GPSの位置情報はほとんど上がってこないといった場合もあるかと思います.また,何かしらのユーザーのアンケートデータを利用した予測を行う場合は,収集したアンケートに未記入項目が出てしまうのはごく自然でしょう.
ナイーブな対処方法としては次の2つ考えられます.1つめとしては,あるデータの一部が欠損している場合は,そのデータごと解析の対称から外してしまうことです.しかし,これは貴重なデータを使わずに捨ててしまっていることになるので,よほどデータ量が潤沢にない限りは非常にもったいないやり方になります.また,継続的に観測される時系列データなどを取り扱う場合には,そもそもうかつにデータを削除することすらできません.2つめの対処法としては,予測アルゴリズムを適用する前に,前処理として線形補間や平均値の当てはめなどを行って欠損を埋めてしまうことです.しかし,こちらの方法も問題があり,前処理で欠損を埋めてしまうと,後段の予測アルゴリズムは受け取ったデータの中の実際に観測された部分と補間された部分の違いが区別できないため,誤った推定結果を出してしまうことになります*1.
ベイズの枠組みで確率的な推論を行えば,データを使った予測と欠損値の補間を同時に行うことができます.補間値に対する不確実性も見積もることもできるため,誤った補間による予測性能の劣化や過学習も基本的には起きません.
ベイズロジスティック回帰
さて,ここではベイズロジスティック回帰を例にいわゆる「教師あり学習」のモデルをおさらいしたいと思います*2.ロジスティック回帰は,多次元の実数値入力データを2値に分類するようなモデルです.入力データ(説明変数)をX,出力データ(目的変数)をY,さらにパラメータをwとすれば,N個のデータに対する同時分布は次のようにモデル化されます*3

ただし,式(1)のそれぞれの分布は次のようになっています.

式(2)のσはシグモイド関数で,中身の実数値を0から1までの間に押し込める役割を担っています.式(3)ではwの事前分布にガウス分布を仮定しています.
このモデルから,下記のパラメータの事後分布に関する特性(平均や分散など)を得ることが,ベイズロジスティック回帰における「学習」にあたります.

式(4)の事後分布はロジスティック回帰の場合では解析可能な表現形式が得られません.ですので,変分ベイズによって何かしらのシンプルな分布で近似をするか,MCMCを使って大量のサンプルを取得することによって平均や分散などを調べる必要があります.
入力データに欠損値がある場合
ここからが本題です.今回は入力データXの一部を,パラメータwと同じようなやり方で推論する必要があるので,次のようにXに対しても事前分布を置いてあげる必要があります.*4

また,ここでは,入力データセットXの任意の部分が欠損しているような状況を考えることにします.あるn番めのデータx_nは,要素の一部が欠損していてもいいですし,まるごと全部無くなっている状態でもOKです.データセットをX={Xo,Xm}のように,観測部分Xoと欠損部分Xmに分解して書けば,求めたい事後分布は次のようになります.

あとは欠損値がなかった場合と同じように,何かしらの近似推論手法を使って式(7)の事後分布の特性を調べてやればOKです.
実験
さて,簡単な2次元のトイデータを使って欠損値補間付きベイズロジスティック回帰の動作を確認してみます.ここでは入力データの次元数をD=2,データ数をN=30とします.また,入力データはそれぞれの要素が50%の割合で欠損しています.今回はスケールの小さい簡単な問題ですので,MCMCの1つであるMetropolis-Hastings法を使用して学習しています.
2クラス分類を行うと,次のような「平均確率の等高線」を描くことができます.
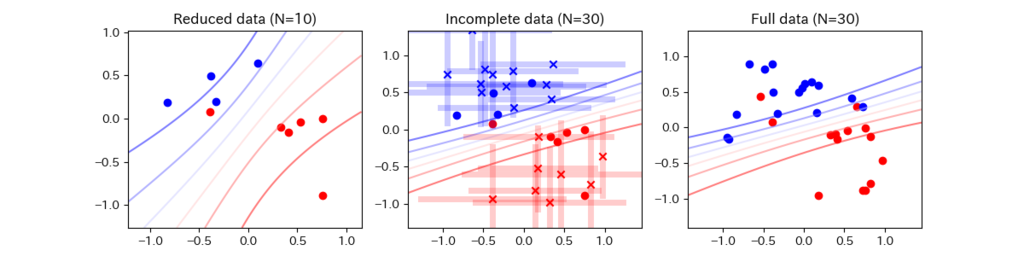
(左図)すべての次元がそろっている場合のデータのみを使った予測結果になります.今回の場合はN=10個のみを使用し,残り20個は捨ててしまった上で学習しています.
(中央図)今回の欠損値補間の方法を用いて,欠損値(×印)を補間推定しながら予測を行った結果です.
(右図)欠損が一切なかった場合の予測結果で,いわば今回の「正解」の予測分布になります.
結果から分かるように,左図では欠損のあるデータを捨ててしまっているので,右図の正解とはほど遠い予測結果になってしまっています.中央図ではx印の点が欠損値を持つデータの推定位置(平均)を表しており,薄い棒はサンプルから計算された推定位置の偏差を表しています.青・赤それぞれのクラスがなんとなくまとまるように配置されている様子が分かりますね.中央図と右図はかなり近い形状の等高線(予測確率)になっており,欠損のあるデータをうまく利活用した方が,データが完全に観測された場合の予測に近づいている様子がわかります.
ランダムではない欠損(追記)
データの持つ値自体と欠損の発生とが因果関係を持つと考えられる場合は,その関係性も確率モデルに組み込むことによって対処できます.これには例えば,「センサーから観測される値が一定の水準を超えると欠損が多くなる」や,「推薦システムにおいて,商品に満足していないユーザーほど評価を行わない」などのケースが考えられます.ベイズでは,このような欠損が発生するプロセスも同時にモデル化することによって対処するのが一般的だと思います.参考として,推薦システムでは次のような文献もあります.
Probabilistic matrix factorization with non-random missing data
まとめ
さて,今回の話を簡単にまとめてみます.
1,データは使えるだけ使った方が良い.
データを捨てるのはもったいないです.アルゴリズムの実装コストや計算コストなどともよく相談する必要がありますが,なるべくなら余計な前処理などせず,上手に単一のモデルから推論できた方が望ましいでしょう.ただし,データの欠損値補間をもっと真剣にやるのであれば,今回のような教師ありモデルを使わずに,生成モデルによってしっかりXをモデル化した方が良いかもしれません.また,問題によっては欠損が発生するメカニズムも同時にモデル化した方がより洗練されたモデルになる可能性もあるでしょう.
2,ベイズの枠組みでは,欠損値もパラメータと同様に確率推論を行う.
「推定したい値はすべて確率変数として扱う」のがベイズの基本です.したがって,教師あり学習を普通に使うときは存在を意識する必要はありませんでしたが,入力の欠損値を推論したい場合は今回のように事前分布を明示的に導入することになります.また,欠損値を確率推論できるようにしておけば,前処理や例外処理をあれこれ実装する手間もなくなります.今回のアルゴリズムであれば,極端な場合入力Xがすべて欠損だったとしても「うまく予測できませんでした」という予測結果が返ってくるだけで,バグになることはありません*5.
3,欠損値の補間を行っても過学習はしない.
ベイズにはそもそも「過学習」という概念すらないので,これはかなりナンセンスな言い方ではあります.仮に,ベイズの代わりに最尤推定を用いて欠損値を推定した場合,尤度を向上させるために際限なく「都合の良い」Xmを求めてしまいます.これは推定というよりも「データの捏造」に近いため,当然ながら新規データに対する汎化性能は期待できません.
今回の実験を行ったソースコード(Julia実装)は下記にあります.(logistic_regression_intrp.jl)
MLBlog/src at master · sammy-suyama/MLBlog · GitHub
今回の記事がよくわからん!という方には,次のような入門書もあります.
*1:僕の経験上最悪のデータは,欠損部分がすでに0で埋められているというものでした.どこが欠損していたかの情報もなかったため,観測値として本当に0なのか,欠損のため0なのか,まったく検討がつきませんでした.
*2:ちなみに,個人的には「教師あり」だとか「教師なし」だとかっていう区別はあんまり本質的ではないと思っています.
*3:ちなみに,個人的には「説明変数」だとか「目的変数」だとかっていう区別はあんまり本質的ではないと思っています.
*4:欠損値がない場合でもXに事前分布を置いても構いませんが,Xがすべて完全に与えられている状況では,結果としてXの事前分布はwの事後分布やyの予測には一切の影響を与えないことが分かります(グラフィカルモデルの記事を参照ください).
*5:より正確に言うと,事前分布の情報のみを使った大雑把な予測を出力してくれます.
変分ベイズを使って変化点検知をしてみる
おつかれさまです.今回は簡単なメッセージ受信数のデータを使って,変分ベイズによる変化点検知をやってみたいと思います.なお,今回使うデータやモデルは下記のPyMCの入門書を参考にしています*1.
Pythonで体験するベイズ推論-PyMCによるMCMC入門-キャメロン-デビッドソン-ピロン
この本では推論にMCMCを使っていますが,今回はモデルはそのまま流用し,同じことを実現する変分ベイズによる近似推論を導いてみます. 一般的には変分ベイズの方が計算が高速なので,MCMCの性能に満足できない場合などは変分ベイズは良い代替手法になり得ます.また,今回紹介する例は,過去に紹介した混合モデルを使った例よりも比較的シンプルですので,変分ベイズの入門題材にはちょうど良いんじゃないかと思っています.
MCMCによる変化点検知
・メッセージ受信データ
PyMC本では次のような「ある期間で受信したメール数」を題材にMCMCを解説しています.

データをよーく見てみると,非常に微妙ではありますが,経過日数の後半の方で受信メッセージ数が少し多くなっているような傾向が見えます.この変化点をベイズモデリングによって見つけるのが目標です.
・モデル
n日目のメッセージ受信数Cnはカウントデータなので,次のようなポアソン分布を使ってモデル化するのが良いでしょう.

ここで,λはポアソン分布の平均パラメータです.また,次のようにある日目を境にこの平均パラメータが変化することを仮定します.

それぞれのパラメータλ1およびλ2はポアソン分布の共役事前分布であるガンマ分布を使ってモデル化します*2.

PyMC本ではデータの平均値を使って超パラメータを設定していますが,あんまりおすすめしません. 僕は適当にa,bの値を設定した後にモデルからデータをサンプルしてみて,なんとなくスケール観が合ってそうな値(a=2.0, b=0.1)に設定しておきました.
最後に,変化点は次のように全部でN日の中から等確率で選ばれると仮定します.
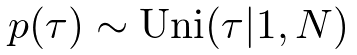
・MCMCによる推論
詳しくは本やJupyter Notebookの内容を参考にしてほしいのですが,モデル(model)をPyMCで構築した後に次のようなコードを書くと事後分布からのサンプルが得られます.
iters = 40000 burn = 10000 mcmc = pm.MCMC(model) mcmc.sample(iters, burn)
mcmc.sampleを叩いたあと,数秒待つと,各変数のサンプルが取り出せます.
lambda_1_samples = mcmc.trace("lambda_1")[:] lambda_2_samples = mcmc.trace("lambda_2")[:] tau_samples = mcmc.trace("tau")[:]
得られたサンプルを元に各種期待値を計算すると,次のようになりました.
 上図ではサンプルから計算される各日のλの期待値をプロットしています.下図では,各日におけるτの近似事後確率を示しています.
確かに,45日目あたりを境に,メッセージ受信数の傾向が微増していることが示唆されていますね.ちなみに,iters=5000より小さい値を設定すると,あんまり綺麗な分布は得られませんでした.
上図ではサンプルから計算される各日のλの期待値をプロットしています.下図では,各日におけるτの近似事後確率を示しています.
確かに,45日目あたりを境に,メッセージ受信数の傾向が微増していることが示唆されていますね.ちなみに,iters=5000より小さい値を設定すると,あんまり綺麗な分布は得られませんでした.
変分ベイズによる変化点検知
・変分ベイズ(平均場近似版)の概要
平均場近似による変分ベイズの導出方法を簡単におさらいしましょう.データXを観測したあとの潜在変数(パラメータ含む)Z1,Z2の事後分布を次のように近似するとします.

Z1,Z2の事後分布を同時分布として表現することは諦め,よりシンプルな独立の分布qで近似しようというのがアイデアです.近似分布qを真の分布に「似せる」ために,次のようなKLダイバージェンスをqに関して最小化します.

詳しくはこちらの記事に書いてありますが,結果としては次のような式を繰り返し計算すればKLダイバージェンスが徐々に小さくなっていくことになります.

今回はこの結果をそのまま使って,変分ベイズのアルゴリズムを導出します.
・更新アルゴリズムの導出
さて,先ほどのメッセージ受信数の変化モデルから,変分ベイズを導いてみることにしましょう.次のように,少しだけモデルを計算しやすく書き直してみます.

ここで,δ()は中身が真の場合は1を返し,そうでない場合は0を返すような関数です.τの値によってデータがサンプルされる分布が切り替わるイメージですね.
次に,このモデルの事後分布の分解を次のように仮定します.

ここまで決めてしまえば,あとは機械的に計算をするだけです.λ1の近似事後分布は,
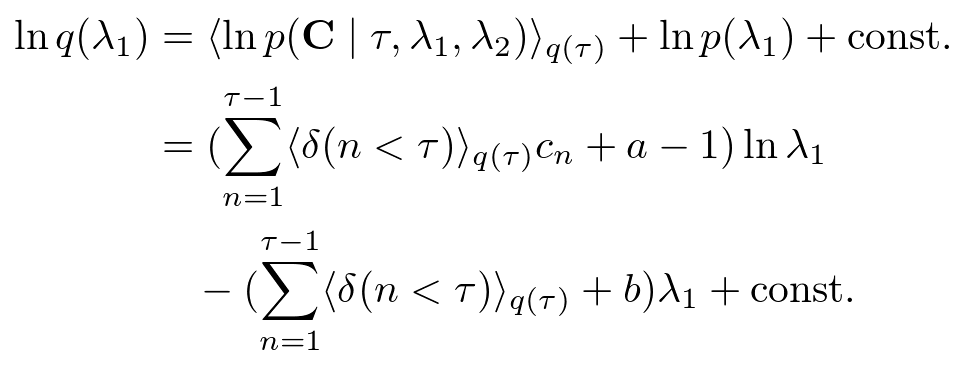
となるので,


とガンマ分布で表現出来ます.λ2もまったく同様に,


となります. 次にτの近似事後分布は,

となるので,次のような離散分布になります.

また,近似事後分布がガンマ分布と離散分布(カテゴリ分布)であることがわかったので,途中計算に必要な期待値も次のように求められます.
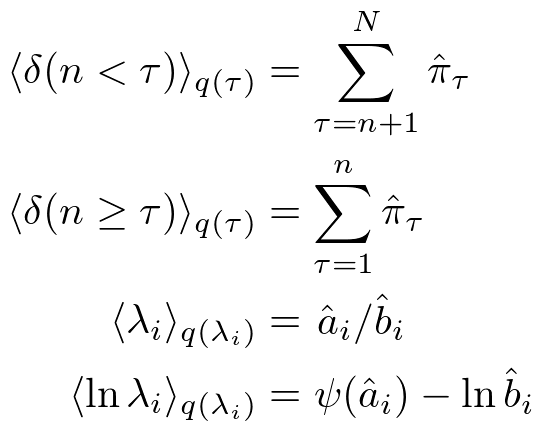
・動かしてみる
さて,先ほどのアルゴリズムを使って事後分布を推定した結果は次のようになります,
 PyMCで十分なサンプル数で実行した場合とほとんど同じ結果になりましたね.ただ,変分ベイズの場合はこの近似分布を得るまでにMAXITER=5程度でほぼ完全に収束し,計算時間も一瞬でした.
PyMCで十分なサンプル数で実行した場合とほとんど同じ結果になりましたね.ただ,変分ベイズの場合はこの近似分布を得るまでにMAXITER=5程度でほぼ完全に収束し,計算時間も一瞬でした.
せっかくなので,適当に作ったトイデータで同じように推論してみます.
 上図からわかるように,変化点がはっきり見えているようなデータなので,下図ではアルゴリズムも確率ほぼ1.0という強い自信を持って変化日が50日目だと言っていますね.
上図からわかるように,変化点がはっきり見えているようなデータなので,下図ではアルゴリズムも確率ほぼ1.0という強い自信を持って変化日が50日目だと言っていますね.
データを作り直してもう1回やってみましょう.
 このデータはちょっと意地悪だったかもしれません.データからはまったく変化点を見ることが出来ません.
下図の結果では「どこかが変化日だったのかわかりません」と言っています.なかなか良い答えです.無理くりどこかを予測結果として出されるより,よっぽど紳士的ですね*3.
このデータはちょっと意地悪だったかもしれません.データからはまったく変化点を見ることが出来ません.
下図の結果では「どこかが変化日だったのかわかりません」と言っています.なかなか良い答えです.無理くりどこかを予測結果として出されるより,よっぽど紳士的ですね*3.
Juliaで実装したソースコードは下記に置いてあります.(change_point.jl)
MLBlog/src at master · sammy-suyama/MLBlog · GitHub
ということで,本日は以上です.
*1:英語になっちゃいますが,本の内容とほぼ同じJupyter Notebookがあります. https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers
*2:PyMC本では指数分布を使っていますが,ガンマ分布でa=1とおけば指数分布に一致します.
*3:今回のモデルは,「変化点は確実に1つあるんだけど,どこかわからない」という前提のもとで推論をする話になっています.最後の結果は「変化点はありませんでした」とは違うことに注意してください.
ベイズ学習の勉強に参考になる資料
おつかれさまです.今回はタイトルの通り,ベイズ学習を勉強する上で参考になる教科書やウェブの資料,論文等を紹介したいと思います.
ベイズ学習は確率推論に基づいた機械学習アルゴリズムの構築論です.ベイズ学習を使えば,あらゆる形式のデータに対して,未観測値の予測や隠れた構造を発見するための統一的なアプローチをとることができるため,特に現代の機械学習アルゴリズムを深く理解し使いこなすためには必須の方法論になっています.
1, ベイズ学習の位置づけ
まず,データサイエンスにおける他の方法論と,ベイズ学習の位置づけを簡単に俯瞰したいと思います.
僕の知る限り,ベイズ学習は1990年代ごろから登場してきた機械学習の方法論で,既存の学習アルゴリズムを確率モデルによって構築し,学習や予測の計算をすべて確率推論(条件付き分布と周辺分布の計算)で解決してしまおうという試みによってはじまりました.これにより,従来の学習アルゴリズムの問題点だった過学習,次元の呪いなどをうまく解決できる(あるいは,問題ですらなかった)ことがわかりました.また,既存の手法がベイズ学習の極めて特別な場合であるとして再定義出来ることが多く,k-means,サポートベクターマシン,ニューラルネットワーク,主成分分析などなど,数え上げればキリがないですが,これらはすべて確率モデルとして再構築でき,従来の学習方法のほとんどは対応する確率モデルに対する特別な近似推論であることが示せます.
ちなみに,最近では深層学習の各種の問題点(大量のデータを必要とする,過学習する,不確実性をハンドル出来ない,ニセのデータに騙される)などをベイズ学習の手法でエレガントに解決する方法が提案され始めているほか,深層学習の各種の計算テクニック(ドロップアウトなど)も実はベイズ学習の近似推論計算であったりすることが発見されています.また,次の動画が参考になりますが,深層学習はベイジアンの目からは「高次元データの多層構造による表現を学習する方法」とされており,グラフィカルモデル*1で表現可能なモデルの一つであるという認識になっています.
さて,すべての未知の値の予測を確率計算のみで行ってしまおうというのがいわゆるベイズ主義とされていますが*2,その反対は頻度主義と呼ばれているようです.したがって,データ解析の分野を俯瞰すれば,「頻度主義 or ベイズ主義」×「統計学 or 機械学習」の組み合わせでおおよそコミュニティが分類できるようです*3.統計学と機械学習の違いは微妙ですが,機械学習の場合は画像や音声などを含めたより複雑な構造のデータを解析対象にする傾向があり,それに伴ってコンピュータを使った効率的な計算の実行に焦点が置かれているようです.頻度主義,ベイズ主義の違いをここでは深入りして説明することはしませんが,もし興味があれば次の動画が参考になると思います.
次にベイズ学習に関連する資料をいくつか挙げていきますが,参考書(PRMLとか)によってはベイズ主義と頻度主義がごちゃごちゃに混ざっている場合があるので,内容を理解するためには十分注意した方が良いでしょう.
2, ベイズ学習を勉強するためのお勧め資料
前置きが長くなってしまいましたが,ここでは主にベイズ学習(ベイズ主義機械学習)を勉強する際に参考になる資料を紹介します.
・PRML
Pattern Recognition and Machine Learning | Christopher Bishop | Springer
Chris Bishopによるベイズ学習の決定版の教科書です.とはいえ,機械学習全体をある程度俯瞰するためにも作られたためか,ベイズではない手法も半分くらい混じっています.次に挙げる章が特に重要です.
- 1,2章の確率計算に関する基本
- 3,4章の回帰・識別の基本
- 8章のグラフィカルモデル
- 9章の混合モデル
- 10,11章の近似推論・サンプリング手法
10章の変分推論が理解できれば,12,13章の各種潜在変数モデルを参考にするよりも,後述のBealの博士論文の方が良いと思います.また,ガウス過程(カーネル)の話もRasmussenのテキストの方が詳しいです.
・BDA
Home page for the book, "Bayesian Data Analysis"
Andrew Gelmanらによるベイズ統計の定番書籍です.統計学の本ですが,各種の確率分布の使い方が解説されているのはもちろん,後半の章では次のような機械学習に深く関連する話題がたくさんあります.
・Machine Learning: A Probabilistic Perspective
Machine Learning | The MIT Press
Kevin Murphyによる,現在出版されている中でも最も網羅的な機械学習の解説書です.ページ数が1000を越えているので,これを使って勉強しようっていう人はあんまりいないと思います.リファレンス的に使うのが良く,僕も崩壊型ギブスサンプリングの解説記事を書くときとかはこの本を参考にしました.
・BRML
David Barber : Brml - Home Page browse
Bayesian Reasoning and Machine Learningの略です.なぜかウェブでフルバージョンのPDFがダウンロード出来ます.
・GPML
Gaussian Processes for Machine Learning: Book webpage
Carl Edward Rasmussenらによるガウス過程の解説書です.
・The Matrix Cookbook
ベイズとは直接関係ないですが,行列の展開や微分計算などの便利な公式がたくさん載っています.
・Variational Algorithms for Approximate Bayesian Inference
Matthew J. Beal - Thesis: Matthew J. Beal, Variational Algorithms for Approximate Bayesian Inference
隠れマルコフモデル等に対する変分推論や初期の平均場近似の使い方の解説記事として良くまとまっています.
・Introduction to Probabilistic Topic Models
http://menome.com/wp/wp-content/uploads/2014/12/Blei2011.pdf
トピックモデルのみの短い解説記事ですが,実際の課題に対してどのように確率モデルを構築・拡張するのか簡単に俯瞰できる内容になっています.
・Nonparametric Bayes Tutorial
http://stat.columbia.edu/~porbanz/npb-tutorial.html
ベイジアンノンパラメトリクスに関する解説記事・論文が網羅されています.
・Probabilistic Modelling and Bayesian Inference
http://mlss.tuebingen.mpg.de/2013/2013/Ghahramani_slides1.pdf
ベイズ学習の解説スライドで,基本的な思想や利点などが説明されています.
まとめ
以上の教科書や解説記事は,それぞれの分野のパイオニアたちが執筆した極めて品質の高い資料であるため,アルゴリズムを開発したり調べ物をする際にはとても参考になると思います.他にも秀逸な記事がありましたらご提案いただけたらと思います.
ただし,ここまで色々挙げといてあれですが,最も大事なことはここで挙げた教科書等を100%完璧に理解してやろうなどと思わないことです.正直なところ,僕も紹介した参考文献の10%~20%くらいしかちゃんと読んでいない気がします.最も効率的なやり方は,業務や研究活動で実際に直面している課題に合わせて,基礎内容の勉強,応用事例の調査,実装と動作の確認をバランス良く繰り返していくことです.そのような実務的なプロセスを通すことによって,アルゴリズム開発者の抱える多くの「○○○がしたい!」にとことん応えてくれるベイズ学習の包容力に気づかされることになると思います.
日本語で書かれた参考文献がほしい!という方には,次のような入門書もあります.
実践!ベイズ学習
今回は、実問題を解くためのベイズ学習による機械学習アルゴリズムの構築方法に関してざっくり俯瞰してみたいと思います。ここで解説するフローは僕が実問題にアプローチする際に意識しているものですが、おそらくこれはベイズ学習のみならず、広く一般的な統計モデリングや機械学習の問題解決にも適用できると思います。
<アルゴリズムの開発フロー>
 あまりファンシーな図でなくて申し訳ないですが、これから1つ1つの項目と各々の遷移に関して説明していきます。
あまりファンシーな図でなくて申し訳ないですが、これから1つ1つの項目と各々の遷移に関して説明していきます。
1、データ・課題の整理をする
まず、機械学習を使って解きたい問題や実現したいサービスを定義してみます。データはあるんだけど何をして良いかわからない、という場合もあるかもしれませんが、そういうときでもとりあえず何かしらの目標を仮置きしてみるのが良いかと思います。基本的に機械学習でできることは「見えない情報の予測」であると考えればアイデアが発想しやすいかもしれません。未来の株価の予測、画像や音声の判別、欠損データの補間、異常値の特定など、これらはすべて未知の事象に対する予測問題として定義することができます。*1
課題が決まれば、次第に必要なデータは明らかになってきます。例えば、明日の東京都全体の電力需要を予測したいのであれば、過去の需要データに加え、その日の天気や曜日の情報(平日or休日)なども予測に役に立つでしょうし、その日に起こる予定のイベントとかも考慮しておいた方が良いかもしれません。この辺りはデータの収集コストと相談する必要もあるかと思います。また、データそのものの収集に伴って、データに関する周辺的な知識(よく知られた法則、物理的な制約など)も色々仕入れておけば、後のモデル構築の段階に役立てられる可能性が高いです。
また、集めたデータの形式や粒度がバラバラだったりする場合はこの時点で揃えておくのが良いかもしれません。ただし、欠損値の補間や異常値の除去、データサイズの補正などのいわゆる「前処理」をここで行ってしまうと、後段のアルゴリズムに対する情報欠損に繋がる可能性があります。手間とコストを十分に考慮する必要がありますが、理想的には、これらの処理はモデルと推論(2および3)で行う方が良いです。
2、モデルを構築する

ここでは確率モデルP(X, Θ)の構築を行います(Xがデータで、Θが学習したいパラメータなどの未観測変数)。基本的なアプローチとしては、「今手元にあるデータXは一体どういうプロセスを経て生成されたのか?*2」ということを念頭に置き、基本的な確率分布を組み合わせてモデルを構築します。
持っているデータの種類によってもモデル構築の仕方が大きく変わってきます。例えばラベルデータを十分に持っているのであれば、既存の教師ありの識別モデル(線形回帰、ロジスティック回帰、ガウス過程など)をそのまま使うのでも良いかもしれません。*3
最も大事なことは、この段階でデータをよく観察し、普遍的な性質や特徴を整理することです。そのような知見をどれだけモデルに組み込むことが出来るかが、未知の値を予測するにあたって非常に重要になってきます。ちなみに、生データに対して何かしらの特徴量抽出を行うやり方も手軽ですが、このような段階を踏んだ情報処理の過程にしてしまうと、その都度情報欠損が起きてしまう可能性があることに注意してください。これを防ぐには、特徴量抽出のプロセスも確率モデルとして組み込むのが理想的です。
さらに、確率モデルを構築した後に必ずやってほしいことは、モデルP(X, Θ)から仮想的にデータXをサンプル(シミュレート)してみることです。このサンプルが、我々が実データを学習させる前に持っている「仮説」を具体的に表していることになります。例えば、データXとして成人男性の身長を仮定しているのに、モデルからサンプルしてみた値が0 cm近辺にへばりついたちっさい値しか出てこないとかいう場合は、明らかにモデル自体か事前分布の設定等が誤っています。モデルからのサンプルが実際に発生し得るデータをちゃんとカバーできそうかどうか、次の推論導出に進む前にチェックしておくのが大事です(「作ったモデルでもっと遊んでね」と僕は表現します)。
3、事後分布を計算する(推論を実行する)
前ステップで構築したモデルをもとに、事後分布P(Θ|X)を評価します。
伝統的な確率推論に対して、機械学習を機械学習たらしめているのはおそらく取り扱う確率モデルの複雑さにあると思います。多くの問題では事後分布が解析的に得られず、推論アルゴリズムを導いてコンピュータ上で実行することになります。具体的にはMCMCや変分近似などの近似推論アルゴリズムを導出してPythonやJulia等の適当な言語で実装するほか、モデルがそれほど複雑でないのであればStanなどのツールを使って自動的に推論してもらうという手もあります。
また、多くの機械学習の課題では、ただパラメータの事後分布を計算するだけを目標とするということはあまりないでしょう。例えば未来の値X*を予測したい場合は、学習された事後分布を使って予測分布P(X*|X)=ΣP(X*, Θ|X)を評価することになると思います。あるいは、クラスタリングなどの「観測することのできない潜在的な値を推定する」問題では、潜在変数モデルP(X,Z,Θ)に対する潜在変数の事後分布P(Z|X)を計算することになります。
ところで、このステップでは多くのバグに苦しむことになります。手で導出した推論アルゴリズムがきちんと動作しているか確認する方法はいくつかあり、一番のオススメとしては、いきなり実データに挑戦せずに、学習前のモデルから仮想的にサンプルしたデータを改めて訓練データとして使って推論させてみることです。このようにすればデータに対するモデルは100%正しいことが保証されるので、推論アルゴリズムの導出式や実装のバグのチェックのみに集中することできます。また他には、例えば変分ベイズ法などの特定の方法では、変分下限と呼ばれる値を評価することにより(ある程度は)動作の正当性を確認できます。
モデル構築および近似推論に関する関連記事は例えば次のようなものがあります。
グラフィカルモデルによる確率モデル設計の基本 - 作って遊ぶ機械学習。
ベイズ混合モデルにおける近似推論① ~変分近似~ - 作って遊ぶ機械学習。
4、結果の評価を行う

作ったアルゴリズムが所望の動作を実現しているか、あるいは改良がうまくいっているかを評価します。モデル自体を評価するような指標(周辺尤度、BIC、AICなど)もありますが、基本的には今解いている課題に即した評価手法を使うのが自然かと思います。例えば連続値の予測であれば二乗誤差で評価するのが(ベストかどうかはともかく)簡単ですし、低頻度のイベントを検知するような課題であればF値を使うのが良いかもしれません。ただし、結果の1%や2%を競うような数値評価至上主義*4に陥らないように注意してください。また、見落としがちではありますが、実際のところ機械学習を使ったサービスなどでは視覚的に結果の良し悪しを確認したり、自分でサービスを使ってみて感触を確かめる、というのも重要な評価手段の1つになります。
それに伴って、アルゴリズムの計算効率(メモリ量や計算速度など)も合わせて評価するのが重要です。というのも、最適化やサンプリングに基づく多くの機械学習アルゴリズムは、時間をかければかけるほど最終的な性能が高くなるものが多く、計算コストを無視した推定精度のみの評価はほとんどの場合では不十分になるためです。
また、機械学習の課題で訓練データとテストデータを分けて評価するのは必須だと思われます(クロスバリデーションなど)。これは過学習をしていないかチェックするための超基本手段なのですが、意外にちゃんとやっていない人が多くてびっくりです。ちなみに「ベイズ学習はそもそも過学習をしないので、データを分けなくても評価できる」という主張もありますが、現実的に多くの場合では近似アルゴリズムを推論に使うことになるので、オーバーフィットやアンダーフィットに近しい現象も起こり得ます。なるべく本番環境に近い状態で評価するためには、やはりテストデータに対する課題依存の評価指標を設定するのが無難かと思います。
確率モデルを使った機械学習アルゴリズムでは、得られた事後分布から仮想的にデータをサンプルしてみるのも学習がうまくいったか直観的にチェックするポイントになります。例えば、顔画像Xを学習する問題を考えてみましょう。事前分布P(Θ)をもとにP(X|Θ)からデータをサンプルしてみると初めはぐちゃぐちゃなノイズしか出てこなかったのが、学習された事後分布P(Θ|X)をもとにサンプルした場合は「顔っぽい」データがちゃんと生成できるようになっているはずです。これがうまくいかない場合は、モデルの表現能力に問題があるか、訓練データ数が少ないか、あるいは推論アルゴリズムの性能が十分でない可能性があります。
よく起こる遷移
・推論導出からモデルの再構築(3→2)
2で構築したモデルが奇怪すぎて推論アルゴリズムがうまく導けない場合があります。
それでも無理やり追加の近似などを仮定してアルゴリズムをひねり出すこともできますが、多くの場合は性能がよくなりません。モデルの構築と推論の導出は分けられたプロセスとして認識すべきですが、実際は相互に行き来しながら一番良い組み合わせを探していくことになります。
・性能評価から推論の再導出(4→3)
アルゴリズムの導出はうまくいっているはずなのに、実データに対して思うような性能が出ない場合は、推論アルゴリズムを再検討してみる必要があります。具体的には、必要メモリ数があまりにも多すぎた場合などは、学習アルゴリズムをオンライン化(Stochastic Gradient Descentなど)してデータを小分けに出来るようにするなどが考えられます。他にも、例えばMCMCが遅すぎる場合は変分近似を使ってみる方が良いかもしれません。
・性能評価からモデルの再構築(4→2)
実験結果を眺めることにより、「うまくモデル化できていない特徴」というのが見えてくる場合があります。この場合は2に戻って、新しい特徴をモデルに組み込むことが必要になってきます。例えば、データに明らかに時間的依存性があることがわかった場合は、モデルをマルコフモデルにするなどの手段が考えられます。
逆に、作ったモデルが複雑すぎるために推論アルゴリズムの性能が出ていない可能性もあります。こういう場合は、ちょっと悔しいですが、モデルから余計な要素を切り落としてシンプル化するのもアリなんじゃないかと思います。
・性能評価から課題の再設定(4→1)
評価結果が思わしくない場合は、データの量や質に関する問題に着目するか、あるいは課題自体を検討しなおしてみるのが良いかもしれません。実際、4の段階にまで入ると、データに関する知識やアルゴリズムの計算コストなども最初の頃よりだいぶ頭に入ってきているはずなので、実運用に基づいた課題の再設定などは積極的に検討すべきなのではないかと思います。
- - -
以上、思いつくままにバァーッと書いてしまいましたが、少しでもベイズ学習あるいは確率モデルによる機械学習構築を検討される際に参考になればと思います。
今回の記事がよくわからん!という方には,次のような入門書もあります.
*1:他にもデータの圧縮、ノイズの除去なども確率モデルの得意とするところです。
*2:いやいや、深層学習とか認識系の課題であれば「データがどういうプロセスを経て認識されたのか」の方が正しいでしょ、とおっしゃる方もいるかもしれません。その場合は、人間が与えるラベルデータが「どのような認識的な処理過程を経て生成されたのか」をモデル化する、と考えれば、文中の言い方でも悪くない気がします。
*3:ところで「教師あり」というのはつまり、「予測したい値と同質と思われるデータを学習用に持っている」とした場合の機械学習の実装方法だと解釈できます。つまり、解きたい実課題自体が教師ありだとか教師なしだとか言うのはナンセンスで、アルゴリズムを開発する人間がその課題をどう捉えるかに依る、というのが正しいと思います。
*4:定量評価というものは、実現したい目標を理解しやすく数値に要約したもの、あるいは仮置きしたものに過ぎません。よっぽど単純な問題でない限り、絶対的な数値評価指標などというものは存在しないと思った方が良いです。